Question

6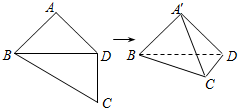．如图，在四边形ABCD中，AB=AD=CD=1，BD=$\sqrt{2}$，BD⊥CD，将四边形ABCD沿对角线BD折成四面体A′BCD，使得平面A′BD⊥平面BDC，给出下列四个结论，其中正确的有（　　）

• A． A′B⊥CD
• B． 四面体A′BCD的体积为$\frac{1}{2}$
• C． A′C与BD所成的角为60°
• D． 四面体A′BCD的外接球的表面积为$\frac{7π}{2}$

Answer 1

分析 利用平面与平面垂直的性质，可得CD⊥平面A′BD，即可得出结论．

解答 解：∵BD⊥CD，平面A′BD⊥平面BDC，平面A′BD∩平面BDC=BD，
∴CD⊥平面A′BD，
∵A′B?平面A′BD，
∴A′B⊥CD，
故选：A，

点评 本题考查平面与平面垂直的性质，考查学生分析解决问题的能力，比较基础．