题目内容
已知命题p:方程x2+y2-2mx+2m2-2m=0表示圆;命题q:双曲线
-
=1的离心率e∈(1,2),若命题“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
| y2 |
| 5 |
| x2 |
| m |
考点:复合命题的真假
专题:简易逻辑
分析:若命题p:方程x2+y2-2mx+2m2-2m=0表示圆为真命题,则(x-m)2+y2=2m-m2>0,解得m范围.若命题q:双曲线
-
=1的离心率e∈(1,2),为真命题,则
∈(1,2),解得m.由于命题“p∧q”为假命题,“p∨q”为真命题,可得p与q必然一真一假.即可得出.
| y2 |
| 5 |
| x2 |
| m |
1+
|
解答:
解:若命题p:方程x2+y2-2mx+2m2-2m=0表示圆为真命题,则(x-m)2+y2=2m-m2>0,解得0<m<2.
若命题q:双曲线
-
=1的离心率e∈(1,2),为真命题,则
∈(1,2),解得0<m<15.
∵命题“p∧q”为假命题,“p∨q”为真命题,
∴p与q必然一真一假.
∴
,或
,
解得2≤m<15或∅.
综上可得:实数m的取值范围是[2,15).
若命题q:双曲线
| y2 |
| 5 |
| x2 |
| m |
1+
|
∵命题“p∧q”为假命题,“p∨q”为真命题,
∴p与q必然一真一假.
∴
|
|
解得2≤m<15或∅.
综上可得:实数m的取值范围是[2,15).
点评:本题考查了双曲线与圆的标准方程及其性质、简易逻辑的判定,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
甲、乙、丙、丁四位同学站成一排照相留念,则甲、乙相邻的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,内角A,B,C所对的边分别为a,b,c,若c2=(a-b)2+6,C=
,则△ABC的面积是( )
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
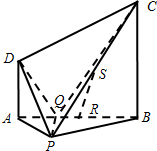 已知四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PA⊥PB,AB=BC=2AD=2PA=2,
已知四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PA⊥PB,AB=BC=2AD=2PA=2,