题目内容
10．若x，y满足约束条件$\left\{\begin{array}{l}x-1≥0\\ x-y≤0\\ x+y-4≤0\end{array}\right.$，则x+2y的取值范围是[3，7] ．分析 利用已知条件画出可行域，关键目标函数的几何意义求最值．
解答 
解：由约束条件得到可行域如图：设z=x+2y则y=$-\frac{1}{2}x+\frac{z}{2}$，当此直线经过图中A（1，1）时直线在y轴的截距最小，z最小，经过C（1，3）时，直线在y轴的截距最大，z最大，所以x+2y的最小值为1+2=3，最大值为1+2×3=7，所以x+2y的取值范围为：[3，7]；
故答案为：[3，7]．
点评 本题考查了简单线性规划问题；首先正确画出可行域，借助于目标函数的几何意义求出最值．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
1．命题“存在x0≥0，${2}^{{x}_{0}}$≤0”的否定是（ ）
| A． | 不存在x0≥0，${2}^{{x}_{0}}$＞0 | B． | 存在x0≥0，${2}^{{x}_{0}}$≥0 | ||
| C． | 对任意的x0≥0，2x≤0 | D． | 对任意的x0≥0，2x＞0 |
18．
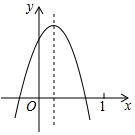已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①b＜0，c＞0；②a+b+c＜0；③方程的两根之和大于0；④a-b+c＜0，其中正确的个数是（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①b＜0，c＞0；②a+b+c＜0；③方程的两根之和大于0；④a-b+c＜0，其中正确的个数是（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
如图，在平面直角坐标系xOy中，点A，B，C分别为坐标轴上的三个点，且OA=1，OB=3，OC=4．
15．已知点（a，b）在圆C：x2+y2=r2（r≠0）的外部，则ax+by=r2与圆C的位置关系是（ ）
| A． | 相切 | B． | 相离 | C． | 内含 | D． | 相交 |
2．北京某小学组织6个年级的学生外出参观包括甲博物馆在内的6个博物馆，每个年级任选一个博物馆参观，则有
且只有两个年级选择甲博物馆的方案有（ ）
且只有两个年级选择甲博物馆的方案有（ ）
| A． | A 6 2×A 5 4种 | B． | A 6 2×5 4种 | C． | C 6 2×A 5 4种 | D． | C 6 2×5 4 |
19．下列命题中，真命题是（ ）
| A． | 所有的素数是奇数 | B． | ?x∈R，x+$\frac{1}{x}$≥2 | ||
| C． | ?x∈R，x2-2x-3=0 | D． | 存在两个相交平面垂直于同一直线 |