题目内容
20.在平面直角坐标系xOy中,以点(0,2)为圆心,且与直线mx-y-3m-1=0(m∈R),相切的所有圆中半径最大的圆的标准方程为x2+(y-2)2=18.分析 求出圆心到直线的距离d的最大值,即可求出所求圆的标准方程.
解答 解:圆心到直线的距离d=$\frac{|-2-3m-1|}{\sqrt{{m}^{2}+1}}$=3$\sqrt{1+\frac{2}{m+\frac{1}{m}}}$≤3$\sqrt{2}$,
∴m=1时,圆的半径最大为3$\sqrt{2}$,
∴所求圆的标准方程为x2+(y-2)2=18.
故答案为:x2+(y-2)2=18.
点评 本题考查所圆的标准方程,考查点到直线的距离公式,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
8.若命题“p且q”为假,且p为真,则( )
| A. | “p或q”为假 | B. | q为假 | C. | q为真 | D. | 不能判断q的真假 |
5.已知N是自然数集,在数轴上表示出集合A,如果所示,则A∩N=( )
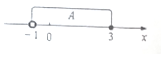

| A. | {-1,0,1,2,3} | B. | {0,1,2,3} | C. | {1,2,3} | D. | {2,3} |
12.已知3x+x3=100,[x]表示不超过x的最大整数,则[x]=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
9.设定义在R上的函数f(x)满足对任意x∈R都有f(x)+f(2-x)=2,若函数g(x)=$\frac{x}{x-1}$与f(x)图象的交点为(x1,y1),(x2,y2),…,(xn,yn),则$\sum_{i=1}^{n}$(xi+yi)=( )
| A. | n | B. | 2n | C. | 3n | D. | 4n |
10.函数f(x)=ax2+4(a+1)x-3在[2,+∞)上递减,则a的取值范围是( )
| A. | a≤-$\frac{1}{2}$ | B. | -$\frac{1}{2}$≤a<0 | C. | 0<a≤$\frac{1}{2}$ | D. | a≥$\frac{1}{2}$ |
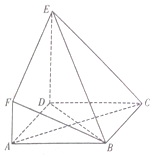 如图,四边形ABCD是正方形,DE⊥平面ABCD,AF∥DE,AF=$\frac{1}{2}AD=\frac{1}{3}$ED=1.
如图,四边形ABCD是正方形,DE⊥平面ABCD,AF∥DE,AF=$\frac{1}{2}AD=\frac{1}{3}$ED=1.