题目内容
甲袋和乙袋中都装有大小相同的红球和白球,已知甲袋中共有m个球,乙袋中共有2m个球.从甲袋中摸出1个球,该球为红球的概率是(1)若m=10,求甲袋中红球的个数;
(2)若将甲、乙两袋中的球装在一起后,从中摸出1个球,该球为红球的概率是![]() ,求P2的值;
,求P2的值;
(3)设P2=![]() ,若从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次.设ξ表示摸出红球的总次数,求ξ的分布列和数学期望.
,若从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次.设ξ表示摸出红球的总次数,求ξ的分布列和数学期望.
解:(1)设甲袋中红球的个数为x,依题意得x=10×![]() =4.
=4.
(2)由已知,得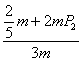 =
=![]() ,解得P2=
,解得P2=![]() .
.
(3)P(ξ=0)=![]() ×
×![]() ×
×![]() =
=![]() ,
,
P(ξ=1)=![]() ×
×![]() ×
×![]() +
+![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() ,
,
P(ξ=2)=![]() ×
×![]() ×
×![]() ×
×![]() +
+![]() ×(
×(![]() )2=
)2=![]() ,
,
P(ξ=3)=![]() ×(
×(![]() )2=
)2=![]() .
.
所以ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
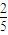 ,从乙袋中摸出1个球为红球的概率为P2.
,从乙袋中摸出1个球为红球的概率为P2. ,求P2的值;
,求P2的值;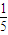 ,若从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次.设ξ表示摸出红球的总次数,求ξ的分布列和数学期望.
,若从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次.设ξ表示摸出红球的总次数,求ξ的分布列和数学期望.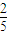 ,从乙袋中摸出1个球为红球的概率为P2.
,从乙袋中摸出1个球为红球的概率为P2. ,求P2的值;
,求P2的值; ,从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次,求摸出的3个球中恰有2个红球的概率.
,从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次,求摸出的3个球中恰有2个红球的概率.