题目内容
甲袋和乙袋中都装有大小相同的红球和白球,已知甲袋中共有m个球,乙袋中共有2m个球,从甲袋中摸出1个球为红球的概率为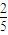 ,从乙袋中摸出1个球为红球的概率为P2.
,从乙袋中摸出1个球为红球的概率为P2.(1)若m=10,求甲袋中红球的个数;
(2)若将甲、乙两袋中的球装在一起后,从中摸出1个红球的概率是
 ,求P2的值;
,求P2的值;(3)设P2=
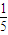 ,若从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次.设ξ表示摸出红球的总次数,求ξ的分布列和数学期望.
,若从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次.设ξ表示摸出红球的总次数,求ξ的分布列和数学期望.
【答案】分析:(1)根据题意设甲袋中红球的个数为x,从甲袋中摸出1个球为红球的概率为 ,根据等可能事件的概率求法做出红球的个数.
,根据等可能事件的概率求法做出红球的个数.
(2)从甲袋中摸出1个球为红球的概率为 ,甲袋中红球的个数
,甲袋中红球的个数 m,从乙袋中摸出1个球为红球的概率为P2.乙袋中有红球2mp2,相加得到红球总数,根据概率列出方程,得到结果.
m,从乙袋中摸出1个球为红球的概率为P2.乙袋中有红球2mp2,相加得到红球总数,根据概率列出方程,得到结果.
(3)由题意知ξ表示摸出红球的总次数,它的取值是0、1、2、3,在两个袋子中摸球相互之间没有影响,所以是相互独立事件同时发生,做出概率,列出分布列,算出期望.
解答:解:(Ⅰ)设甲袋中红球的个数为x,
∵从甲袋中摸出1个球为红球的概率为 ,
,
∴依题意得x=10× =4.
=4.
(Ⅱ)∵从甲袋中摸出1个球为红球的概率为 ,
,
∴甲袋中红球的个数 m,
m,
∵从乙袋中摸出1个球为红球的概率为P2.
∴乙袋中有红球2mp2
由已知得: ,
,
解得P2= .
.
(Ⅲ)由题意知ξ表示摸出红球的总次数,它的取值是0、1、2、3,
在两个袋子中摸球相互之间没有影响,所以是相互独立事件同时发生,
∴ ,
,
 ,
,
 ,
,
 .
.
∴ξ的分布列为

∴Eξ=0× +1×
+1× +2×
+2× +3×
+3× =
= .
.
点评:本题考查概率和期望以及它们的实际应用,期望是概率论和数理统计的重要概念之一,是反映随机变量取值分布的特征数,学习期望将为今后学习概率统计知识做铺垫.
 ,根据等可能事件的概率求法做出红球的个数.
,根据等可能事件的概率求法做出红球的个数.(2)从甲袋中摸出1个球为红球的概率为
 ,甲袋中红球的个数
,甲袋中红球的个数 m,从乙袋中摸出1个球为红球的概率为P2.乙袋中有红球2mp2,相加得到红球总数,根据概率列出方程,得到结果.
m,从乙袋中摸出1个球为红球的概率为P2.乙袋中有红球2mp2,相加得到红球总数,根据概率列出方程,得到结果.(3)由题意知ξ表示摸出红球的总次数,它的取值是0、1、2、3,在两个袋子中摸球相互之间没有影响,所以是相互独立事件同时发生,做出概率,列出分布列,算出期望.
解答:解:(Ⅰ)设甲袋中红球的个数为x,
∵从甲袋中摸出1个球为红球的概率为
 ,
,∴依题意得x=10×
 =4.
=4.(Ⅱ)∵从甲袋中摸出1个球为红球的概率为
 ,
,∴甲袋中红球的个数
 m,
m,∵从乙袋中摸出1个球为红球的概率为P2.
∴乙袋中有红球2mp2
由已知得:
 ,
,解得P2=
 .
.(Ⅲ)由题意知ξ表示摸出红球的总次数,它的取值是0、1、2、3,
在两个袋子中摸球相互之间没有影响,所以是相互独立事件同时发生,
∴
 ,
, ,
, ,
, .
.∴ξ的分布列为

∴Eξ=0×
 +1×
+1× +2×
+2× +3×
+3× =
= .
.点评:本题考查概率和期望以及它们的实际应用,期望是概率论和数理统计的重要概念之一,是反映随机变量取值分布的特征数,学习期望将为今后学习概率统计知识做铺垫.

练习册系列答案
相关题目
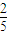 ,从乙袋中摸出1个球为红球的概率为P2.
,从乙袋中摸出1个球为红球的概率为P2. ,求P2的值;
,求P2的值; ,从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次,求摸出的3个球中恰有2个红球的概率.
,从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次,求摸出的3个球中恰有2个红球的概率.