题目内容
 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0)(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0)(6,4),则f(f(0))=2
2
;函数f(x)在x=1处的导数 f′(x)=-2
-2
;函数f(x)的极值点是2
2
;| ∫ | 6 0 |
12
12
.分析:函数f(x)的图象是折线段ABC,其中A,B,C,由图象找出函数的整点,根据这些对应关系求f(f(0));由函数的图象可知,y=
,由此能求出函数f(x)在x=1处的导数;观察图形,知函数f(x)在x=2处取得极小值;由y=
,能求出
f(x)dx.
|
|
| ∫ | 6 0 |
解答:解:观察图形,得f(0)=4,f(4)=2,
∴f(f(0))=2.
∵f(0)=4,f(4)=2,f(2)=4,
∴由函数的图象可知,
y=
,
当0≤x≤2时,f'(x)=-2
∴f'(1)=-2;
观察图形,知函数f(x)在x=2处取得极小值0,
∴函数f(x)的极值点是2;
∵f(x)=
,
∴
f(x)dx=(-x2+4x)
+(
x2-2x)
=(-4+8)+[(
×36-2×6)-(
×4-2×2)]=12.
故答案为:2,-2,2,12.
∴f(f(0))=2.
∵f(0)=4,f(4)=2,f(2)=4,
∴由函数的图象可知,
y=
|
当0≤x≤2时,f'(x)=-2
∴f'(1)=-2;
观察图形,知函数f(x)在x=2处取得极小值0,
∴函数f(x)的极值点是2;
∵f(x)=
|
∴
| ∫ | 6 0 |
| | | 2 0 |
| 1 |
| 2 |
| | | 6 2 |
=(-4+8)+[(
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:2,-2,2,12.
点评:本题考查求函数的值,解题的关键是看懂函数的图象,由图象找出自变量与函数值的对应,求出函数的值.主要考查了分段函数的函数值的求解,解题的关键是根据已知的点求解出AB,BC的直线方程,进而写出分段函数f(x)的解析式.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 4、如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(1))=
4、如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(1))= 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(2))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(2))= 如图,函数f(x)的图象为单位圆上的两段弧,求不等式f(x)-f(-x)>x的解集.
如图,函数f(x)的图象为单位圆上的两段弧,求不等式f(x)-f(-x)>x的解集. 如图,函数f(x)的图象是折线段ABC,其中A(0,4),B(2,0),C(6,4),则f(f(
如图,函数f(x)的图象是折线段ABC,其中A(0,4),B(2,0),C(6,4),则f(f(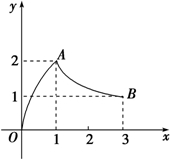 (2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(
(2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(