题目内容
 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(2))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(2))=4
4
; 函数f(x)在x=3处的导数f′(3)=1
1
.分析:(1)要求f(f(2))的值,可先求f(2)=0,再求f(0),此即为所求;
(2)函数的图象可知,y=
,然后求出导数即可求出结果.
(2)函数的图象可知,y=
|
解答:解:(1)由图象可知f(2)=0,f(0)=4,
即f(f(2))=4.
(2)∵f(0)=4,f(4)=2,f(2)=4,
∴由函数的图象可知,
y=
,
当2≤x≤6时,f'(x)=1,
∴f'(3)=1.
故答案为:4,1.
即f(f(2))=4.
(2)∵f(0)=4,f(4)=2,f(2)=4,
∴由函数的图象可知,
y=
|
当2≤x≤6时,f'(x)=1,
∴f'(3)=1.
故答案为:4,1.
点评:本题考查函数的图象,导数的运算,解题时要注意分段函数的定义域,属于基础题.

练习册系列答案
相关题目
 4、如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(1))=
4、如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(1))= 如图,函数f(x)的图象为单位圆上的两段弧,求不等式f(x)-f(-x)>x的解集.
如图,函数f(x)的图象为单位圆上的两段弧,求不等式f(x)-f(-x)>x的解集. 如图,函数f(x)的图象是折线段ABC,其中A(0,4),B(2,0),C(6,4),则f(f(
如图,函数f(x)的图象是折线段ABC,其中A(0,4),B(2,0),C(6,4),则f(f(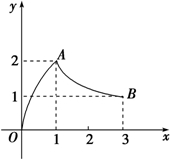 (2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(
(2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(