题目内容
 如图,函数f(x)的图象为单位圆上的两段弧,求不等式f(x)-f(-x)>x的解集.
如图,函数f(x)的图象为单位圆上的两段弧,求不等式f(x)-f(-x)>x的解集.分析:f(x)=
=
,由此进行分类讨论,能求出不等式f(x)-f(-x)>x的解集.
| x |
| |x| |
| 1-x2 |
|
解答:解:f(x)=
=
①当0<x≤1时,f(x)=
,
f(-x)=-
=-
.
由f(x)-f(-x)>x.
则2
>x>0.4-4x2>x2,x2<
.
∵0<x≤1.∴0<x<
(6分)
②当-1≤x<0时,f(x)=-
,
f(-x)=
=
,
f(x)-f(-x)>x,
即-2
>x,即2
<-x,即4-4x2<x2,即x2>
.
∵-1≤x<0,∴-1≤x<-
.
由①②知原不等式的解集为{x|-1≤x<-
,或0<x<
}.(12分)
| x |
| |x| |
| 1-x2 |
=
|
①当0<x≤1时,f(x)=
| 1-x2 |
f(-x)=-
| 1-(-x)2 |
| 1-x2 |
由f(x)-f(-x)>x.
则2
| 1-x2 |
| 4 |
| 5 |
∵0<x≤1.∴0<x<
2
| ||
| 5 |
②当-1≤x<0时,f(x)=-
| 1-x2 |
f(-x)=
| 1-(-x)2 |
| 1-x2 |
f(x)-f(-x)>x,
即-2
| 1-x2 |
| 1-x2 |
| 4 |
| 5 |
∵-1≤x<0,∴-1≤x<-
2
| ||
| 5 |
由①②知原不等式的解集为{x|-1≤x<-
2
| ||
| 5 |
2
| ||
| 5 |
点评:本题考查不等式的解法,综合性强,难度大,有一定的探索性.解题时要认真审题,仔细解答,注意分段函数的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 4、如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(1))=
4、如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(1))= 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(2))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(2))= 如图,函数f(x)的图象是折线段ABC,其中A(0,4),B(2,0),C(6,4),则f(f(
如图,函数f(x)的图象是折线段ABC,其中A(0,4),B(2,0),C(6,4),则f(f(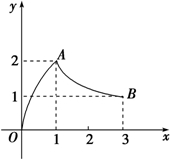 (2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(
(2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(