题目内容
7.如图所示,由若干个点组成形如三角形的图形,每条边(包括两个端点)有n(n>1,n∈N)个点,每个图形总的点数记为an,则a6=15;$\frac{9}{{{a_2}{a_3}}}$+$\frac{9}{{{a_3}{a_4}}}$+$\frac{9}{{{a_4}{a_5}}}$+…+$\frac{9}{{{a_{2015}}{a_{2016}}}}$=$\frac{2014}{2015}$.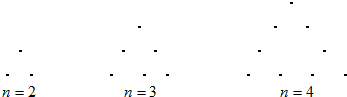
分析 根据图象的规律可得出通项公式an,根据数列的特点可用列项法求其前n项和的公式,而$\frac{9}{{{a_2}{a_3}}}$+$\frac{9}{{{a_3}{a_4}}}$+$\frac{9}{{{a_4}{a_5}}}$+…+$\frac{9}{{{a_{2015}}{a_{2016}}}}$是前2014项的和,代入前n项和公式即可得到答案.
解答 解:每个边有n个点,把每个边的点数相加得3n,这样角上的点数被重复计算了一次,故第n个图形的点数为3n-3,即an=3n-3,∴a6=15;
令Sn=$\frac{1}{1×2}+\frac{1}{2×3}$+…+$\frac{1}{2014×2015}$=1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$=$\frac{2014}{2015}$.
故答案为15;$\frac{2014}{2015}$
点评 本题主要考查简单的和清推理,求等差数列的通项公式和用裂项法对数列进行求和问题,同时考查了计算能力,属中档题.

练习册系列答案
相关题目
18.为了调查每天微信用户使用微信的时间,某经销化妆品分微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜各1份,再从抽取的这5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为X,试求X的分布列和数学期望.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
参考数据:
| 微信控 | 非微信控 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜各1份,再从抽取的这5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为X,试求X的分布列和数学期望.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
参考数据:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
2.已知f(x)为定义在(-∞,+∞)上的可导函数,且f(x)>f′(x)对于x∈R恒成立(e为自然对数的底),则( )
| A. | e2015•f(2016)>e2016•f(2015) | |
| B. | e2016•f(2016)=e2016•f(2015) | |
| C. | e2015•f(2016)<e2016•f(2015) | |
| D. | e2015•f(2016)与e2016•f(2015)大小不确定 |