题目内容
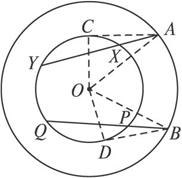
 图中的同心圆,大⊙O的弦AB切小⊙O于P,且AB=6,则圆环的面积为
图中的同心圆,大⊙O的弦AB切小⊙O于P,且AB=6,则圆环的面积为
- A.9π
- B.8π
- C.4π
- D.π
A
分析:已知大⊙O的弦AB切小⊙O于P,则OA2-OP2=AP2=( AB)2=9,因为圆环的面积=πOA2-πOP2=(OA2-OP2)π=9π.
AB)2=9,因为圆环的面积=πOA2-πOP2=(OA2-OP2)π=9π.
解答:连接OA、OP;
∵同心圆大⊙O的弦AB切小⊙O于P,
∴∠OPA=90°,AP= AB=3,
AB=3,
∴圆环的面积=πOA2-πOP2=(OA2-OP2)π=9π.
故选A.
点评:此题主要考查学生对切线的性质及勾股定理的理解运用.
分析:已知大⊙O的弦AB切小⊙O于P,则OA2-OP2=AP2=(
 AB)2=9,因为圆环的面积=πOA2-πOP2=(OA2-OP2)π=9π.
AB)2=9,因为圆环的面积=πOA2-πOP2=(OA2-OP2)π=9π.解答:连接OA、OP;
∵同心圆大⊙O的弦AB切小⊙O于P,
∴∠OPA=90°,AP=
 AB=3,
AB=3,∴圆环的面积=πOA2-πOP2=(OA2-OP2)π=9π.
故选A.
点评:此题主要考查学生对切线的性质及勾股定理的理解运用.

练习册系列答案
相关题目
 图中的同心圆,大⊙O的弦AB切小⊙O于P,且AB=6,则圆环的面积为 ( )
图中的同心圆,大⊙O的弦AB切小⊙O于P,且AB=6,则圆环的面积为 ( )| A、9π | B、8π | C、4π | D、π |