题目内容
如图，在以O为圆心的两个同心圆中，A、B是大圆上任意两点，过A、B作小圆的割线AXY和BPQ.求证：AX·AY=BP·BQ.
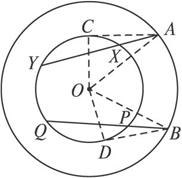
思路点拨：在平面几何比较复杂的图形中，往往都是由几个简单的图形组合而成的.但本题不直接含有这样的图形，我们应考虑通过添加适当的辅助线来构造出这样的图形，以此为出发点，经探索可得出以下几种不同的辅助线的添法.
证明：如图，过点A、B分别作小圆的切线AC、BD，C、D为切点.这时就出现了切割线定理的基本图形，于是有AC2＝AX·AY，BD2＝BP·BQ.
再连结CO、AO、DO、BO，
易证Rt△AOC≌Rt△BOD，得出AC＝BD.
所以AX·AY＝BP·BQ.
练习册系列答案
阅读快车系列答案
相关题目
通常用a、b、c分别表示△ABC的三个内角A，B，C所对边的边长，R表示△ABC的外接圆半径．
（I）A为△ABC的内角，则sinA+cosA的取值范围是
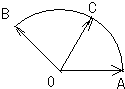（2011•重庆模拟）给定两个长度均为2的平面向量