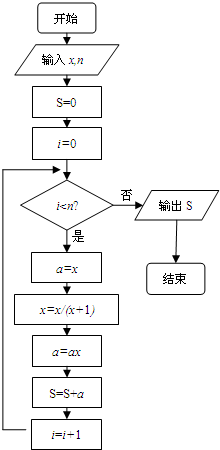
题目内容
9.等差数列{an}的前n项和为Sn,若a1,a3,a4成等比数列,则$\frac{{S}_{3}-{S}_{2}}{{S}_{5}-{S}_{3}}$的值为( )| A. | 1或2 | B. | $\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$或2 |
分析 设等差数列{an}的公差为d,由a1,a3,a4成等比数列,可得${a}_{3}^{2}={a}_{1}{a}_{4}$,即$({a}_{1}+2d)^{2}={a}_{1}({a}_{1}+3d)$,化为a1=-4d≠0,或d=0.代入即可得出.
解答 解:设等差数列{an}的公差为d,
∵a1,a3,a4成等比数列,
∴${a}_{3}^{2}={a}_{1}{a}_{4}$,
即$({a}_{1}+2d)^{2}={a}_{1}({a}_{1}+3d)$,
化为a1=-4d≠0,或d=0.
则$\frac{{S}_{3}-{S}_{2}}{{S}_{5}-{S}_{3}}$=$\frac{{a}_{3}}{{a}_{4}+{a}_{5}}$=$\frac{{a}_{1}+2d}{2{a}_{1}+7d}$=$\frac{-4d+2d}{-4d+7d}$=2,
或$\frac{{S}_{3}-{S}_{2}}{{S}_{5}-{S}_{3}}$=$\frac{{a}_{3}}{{a}_{4}+{a}_{5}}$=$\frac{{a}_{1}+2d}{2{a}_{1}+7d}$=$\frac{1}{2}$.
故选:D.
点评 本题考查了等差数列与等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.定义在R上的函数g(x)=ex+e-x+|x|,则满足g(2x-1)<g(3)的x的取值范围是( )
| A. | (-∞,2) | B. | (-2,2) | C. | (-1,2) | D. | (2,+∞) |
20.若圆x2+y2+2kx+2y+2=0(k>0)与两坐标轴无公共点,那么实数k的取值范围是( )
| A. | 0<k<$\sqrt{2}$ | B. | 1<k<$\sqrt{2}$ | C. | 0<k<1 | D. | k>$\sqrt{2}$ |
4.等差数列{an}中,a1+a3+a5=π,则cosa3=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |