题目内容
17.定义:若对于平面点集A中的任意一个点(x0,y0),总存在正实数r,使得集合{(x,y)|$\sqrt{(x-{x}_{0})^{2}+(y-{y}_{0})^{2}}$<r}⊆A,则称A为一个开集,给出下列集合:①{(x,y)|x2+y2<1}; ②{(x,y)|x+y≥2};
③{(x,y)||x+y|≤5}; ④{(x,y)|$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1}.
其中为开集的是①.(写出所有符合条件的序号).
分析 弄清开集的定义是解决本题的关键.即所选的集合需要满足存在以该集合内任意点为圆心,任意正实数为半径的圆内部分均在该集合内.初步确定该集合不含边界.
解答 解:由题意,所选的集合需要满足存在以该集合内任意点为圆心,任意正实数为半径的圆内部分均在该集合内,且该集合不含边界.
对于①,只要半径足够小即可,故①是开集;
对于②③④,含边界,不是开集.
故答案为:①.
点评 本题属于集合的新定义型问题,考查学生即时掌握信息,解决问题的能力.正确理解好集的定义是解决本题的关键.

练习册系列答案
相关题目
8.已知幂函数y=f(x)的图象经过点(2,8),则f(3)的值为( )
| A. | 9 | B. | 27 | C. | 64 | D. | 16$\sqrt{2}$ |
5.已知集合A={x|log${\;}_{\frac{1}{2}}$x<0},集合B={x|10x>1},则A∩B=( )
| A. | {x|x>1} | B. | {x|x>0} | C. | {x|x>1}∪{x|x<0} | D. | ∅ |
12.已知F1,F2为双曲线C的左右焦点,过F1的直线分别交C的左右两支于A,B两点,若△AF2B为等腰直角三角形,且∠AF2B=90°,那么C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
9.等差数列{an}的前n项和为Sn,若a1,a3,a4成等比数列,则$\frac{{S}_{3}-{S}_{2}}{{S}_{5}-{S}_{3}}$的值为( )
| A. | 1或2 | B. | $\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$或2 |
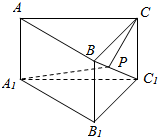 在直三棱柱ABC-A1B1C1中,底面为直角三角∠ACB=90°,AC=$\sqrt{2}$,BC=CC1=1,P是BC1上一动点,则A1P+PC的最小值是$\sqrt{5}$.
在直三棱柱ABC-A1B1C1中,底面为直角三角∠ACB=90°,AC=$\sqrt{2}$,BC=CC1=1,P是BC1上一动点,则A1P+PC的最小值是$\sqrt{5}$.