题目内容
如图,F1,F2分别是椭圆C: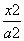 +
+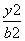 =1(a>b>0)的左、右焦点,
=1(a>b>0)的左、右焦点,
A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.且△AF1B的面积为40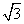 ,
,
则a=________,b=________.
10 5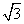
解析 (1)左焦点为F1(-c,0),PF1⊥x轴,
当x=-c时,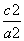 +
+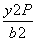 =1⇒y
=1⇒y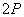 =b2
=b2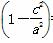 =
=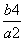 ⇒yP=
⇒yP=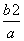 (负值不合题意,已舍去),点P
(负值不合题意,已舍去),点P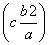 ,
,
由斜率公式得kAB=-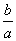 ,kOP=-
,kOP=-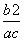 .
.
∵AB∥OP,∴kAB=kOP⇒-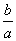 =-
=-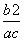 ⇒b=c.
⇒b=c.
∵a2=b2+c2=2c2,
∴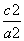 =
=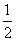 ⇒e=
⇒e=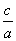 =
=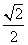 .
.
(2)法一 a2=4c2,b2=3c2,直线AB的方程为y=-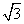 (x-c),
(x-c),
将其代入椭圆方程3x2+4y2=12c2,得B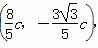 ,
,
所以|AB|=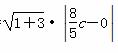 =
=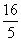 c.
c.
由S△AF1B=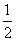 |AF1|·|AB|·sin∠F1AB=
|AF1|·|AB|·sin∠F1AB=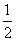 a·
a·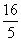 c·
c·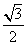 =
=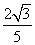 a2=40
a2=40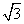 ,解得a=10,b=5
,解得a=10,b=5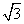 .
.
法二 设|AB|=t(t>0).
因为|AF2|=a,所以|BF2|=t-a.
由椭圆定义|BF1|+|BF2|=2a可知,|BF1|=3a-t,
再由余弦定理(3a-t)2=a2+t2-2atcos 60°可得,t=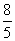 a.
a.
由S△AF1B=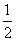 a·
a·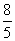 a·
a·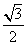 =
=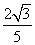 a2=40
a2=40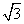 知,
知,
a=10,b=5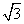 .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
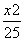 +
+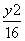 =1的左、右焦点,P为椭 圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点的 距离为 ( ).
=1的左、右焦点,P为椭 圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点的 距离为 ( ). 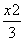 +y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( ).
+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( ).