题目内容
某地区因干旱缺水,政府向市民宣传节约用水,并进行广泛动员. 三个月后,统计部门在一个小区随机抽取了100户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示).


(Ⅰ)已知该小区共有居民10000户,在政府进行节水动员前平均每月用水量是8.96×104吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨.
(Ⅱ)为了解动员前后市民的节水情况,媒体计划在上述家庭中,从政府动员前月均用水量在 范围内的家庭中选出5户作为采访对象,其中在
范围内的家庭中选出5户作为采访对象,其中在 内的抽到
内的抽到 户,求
户,求 的分布列和期望.
的分布列和期望.
(Ⅰ)根据直方图估计该小区在政府动员后平均每户居民的月均用水量为
(1×0.015+3×0.030+5×0.105+7×0.200+9×0.120+11×0.030)×2=6.88(吨).
于是可估计该小区在政府动员后比动员前平均每月可节约用水:
8.96×104-6.88×104=2.08×104(吨).
(Ⅱ)由动员前的直方图计算得月平均用水量在[12,14)范围内的家庭有6户,在[14,16)范围内的有3户,因此X的可能取值有0,1,2,3,
 ,
, ,
, ,
,
所以X的分布列为
| X | 0 | 1 | 2 | 3 |
| P |
|
|
|
|

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目




 满足
满足 ,则
,则 的最大值为 .
的最大值为 . 展开式中的所有二项式系数和为64,则该展开式中的含
展开式中的所有二项式系数和为64,则该展开式中的含 的系数为 ____。
的系数为 ____。 函数
函数 的图象大致为( )
的图象大致为( ) .
.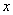 的不等式
的不等式 ;
; 对任意的实数
对任意的实数 的取值范围.
的取值范围. A.
A.



 B.
B.
 D.
D.
 ”是“函数
”是“函数 上是增函数”的
上是增函数”的