题目内容
2.已知圆M:(x-1)2+(y-3)2=1,圆N:(x-7)2+(y-5)2=4,点P,Q分别为圆M和圆N上一点,点A是x轴上一点,则|AP|+|AQ|的最小值为7.分析 由题意,M(1,3),N(7,5),M关于x轴的对称点的坐标为M′(1,-3),求出|M′N|,即可得出结论.
解答 解:由题意,M(1,3),N(7,5),M关于x轴的对称点的坐标为M′(1,-3),
∴|M′N|=$\sqrt{(7-1)^{2}+(5+3)^{2}}$=10,
∴|AP|+|AQ|=|M′N|-1-2=7,
故答案为7.
点评 本题考查圆与圆的位置关系,考查对称性的运用,正确转化是关键.

练习册系列答案
相关题目
13.设Sn为等差数列{an}的前n项和,a1=-2,S3=0,则{an}的公差为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.已知两条不同直线a,b及平面α,则下列命题中真命题是( )
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥b,b∥α,则a∥α | C. | 若a⊥α,b⊥α,则a∥b | D. | 若a⊥α,b⊥a,则b⊥α |
7.已知圆C1:x2+y2-2mx+m2=4,圆C2:x2+y2+2x-2my=8-m2(m>3),则两圆的位置关系是( )
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 外离 |
14.设$a={({\frac{1}{2}})^{\frac{1}{2}}},b={({\frac{1}{2}})^{\frac{1}{3}}},c={log_{\frac{1}{2}}}2$,则( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
12.已知随机变量ξ服从二项分布$ξ~B({6,\frac{1}{3}})$,即P(ξ=2)等于( )
| A. | $\frac{3}{16}$ | B. | $\frac{1}{243}$ | C. | $\frac{13}{243}$ | D. | $\frac{80}{243}$ |
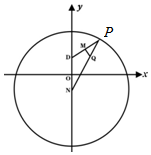 如图,已知圆N:x2+(y+$\sqrt{5}$)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,$\sqrt{5}$)和DP上的点M,满足$\overrightarrow{DP}$=2$\overrightarrow{DM}$,$\overrightarrow{MQ}$•$\overrightarrow{DP}$=0.
如图,已知圆N:x2+(y+$\sqrt{5}$)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,$\sqrt{5}$)和DP上的点M,满足$\overrightarrow{DP}$=2$\overrightarrow{DM}$,$\overrightarrow{MQ}$•$\overrightarrow{DP}$=0.