题目内容
如图,正方形ABCD和三角形ACE所在的平面互相垂直,EF∥BD,AB= EF.
EF.

(1)求证:BF∥平面ACE;
(2)求证:BF⊥BD.
证明 (1)AC与BD交于O点,连接EO.
正方形ABCD中, BO
BO =AB,又因为AB=
=AB,又因为AB= EF
EF ,
,
 ∴BO=EF,又因为EF∥BD,
∴BO=EF,又因为EF∥BD,
∴EFBO是平行四边形,
∴BF∥EO,又∵BF⊄平面ACE,EO⊂平面ACE,
∴BF∥平面ACE.(7分)
(2)正方形ABCD中,AC⊥BD,又因为正方形ABCD和三角形ACE所在的平面互相垂直,BD⊂平面ABCD,平面ABCD∩平面ACE=AC,
∴BD⊥平面ACE,∵EO⊂平面ACE,
∴BD⊥EO,∵EO∥BF,∴BF⊥BD.(14分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在曲线
在曲线 上”是“点
上”是“点 ”的 条件.
”的 条件. 的图象关于点(1,0)中心对称,则a的值为_______
的图象关于点(1,0)中心对称,则a的值为_______
 x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)
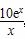 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)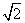 )cm2 B. 21 cm2 C.(24+4
)cm2 B. 21 cm2 C.(24+4

 c.28+
c.28+ D.26+2
D.26+2

 ,
, ,
, ,则
,则  B.
B.  C.
C. D.
D.