题目内容
△ABC的角A、B、C所对的边分别为a、b、c,已知a=5、b=7、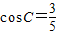 .
.(1)求△ABC的面积S;
(2)求c边上的高h.
【答案】分析:(1)利用同角三角函数的关系,算出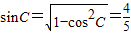 ,再由正弦定理的面积公式即可算出△ABC的面积S;
,再由正弦定理的面积公式即可算出△ABC的面积S;
(2)根据余弦定理算出边c的长,再利用三角形面积公式得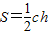 ,代入数据即可求出c边上的高h的大小.
,代入数据即可求出c边上的高h的大小.
解答:解:(1)∵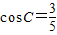 ,0<C<π,
,0<C<π,
∴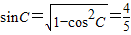 …(3分)
…(3分)
所以,△ABC的面积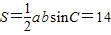 …(6分)
…(6分)
(2)根据余弦定理,得
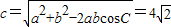 …(9分)
…(9分)
根据三角形面积公式得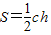 ,
,
∴c边上的高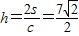 …(12分)
…(12分)
点评:本题给出三角形ABC的两边和夹角的余弦,求它的面积和第3边上的高.着重考查了三角形的面积公式、同角三角函数的关系和正余弦定理等知识,属于基础题.
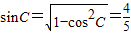 ,再由正弦定理的面积公式即可算出△ABC的面积S;
,再由正弦定理的面积公式即可算出△ABC的面积S;(2)根据余弦定理算出边c的长,再利用三角形面积公式得
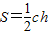 ,代入数据即可求出c边上的高h的大小.
,代入数据即可求出c边上的高h的大小.解答:解:(1)∵
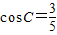 ,0<C<π,
,0<C<π,∴
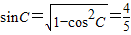 …(3分)
…(3分)所以,△ABC的面积
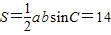 …(6分)
…(6分)(2)根据余弦定理,得
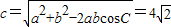 …(9分)
…(9分)根据三角形面积公式得
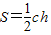 ,
,∴c边上的高
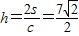 …(12分)
…(12分)点评:本题给出三角形ABC的两边和夹角的余弦,求它的面积和第3边上的高.着重考查了三角形的面积公式、同角三角函数的关系和正余弦定理等知识,属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
若△ABC的角A,B,C对边分别为a、b、c,且a=1,∠B=45°,S△ABC=2,则b=( )
| A、5 | ||
| B、25 | ||
C、
| ||
D、5
|
△ABC的角A,B,C的对边分别为a,b,c,已知b=4,B=
,C=
,则c的长度是( )
| π |
| 3 |
| π |
| 4 |
A、
| ||||
B、2
| ||||
C、
| ||||
D、2
|