题目内容
(本小题满分12分)如图1,在Rt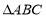 中,
中,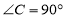 ,
,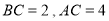 .
.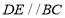 ,将
,将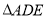 沿
沿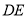 折起到
折起到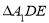 的位置,使
的位置,使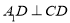 ,如图2.
,如图2.

(Ⅰ)求证: 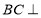 平面
平面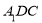 ;
;
(Ⅱ)若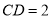 ,求平面
,求平面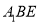 与平面
与平面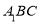 所成二面角的大小.
所成二面角的大小.
(1)见解析;(2) .
.
【解析】
试题分析:(1)由折起过程可知 ,所以
,所以 平面
平面 ,又
,又 ,可证;(2)建立空间直角坐标系,由空间向量直接计算二面角的大小即可.
,可证;(2)建立空间直角坐标系,由空间向量直接计算二面角的大小即可.
试题解析:(Ⅰ)证明: 在△ 中,
中,
 .又
.又 .
.
由
 . 5分
. 5分
(Ⅱ)如图,以 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系 .取A1C的中点F,连DF,
.取A1C的中点F,连DF,

则 

由(1)可知, , 从而
, 从而 

 为平面
为平面 的法向量,
的法向量,
又  ,
,
设平面 的法向量为
的法向量为
由 


 平面
平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为  12分
12分
考点:线面垂直的判定与性质、空间向量的应用.

练习册系列答案
相关题目
已知某地区中小学生人数和近视情况如下表所示:
年级 | 人数 | 近视率 |
小学 | 3500 | 10% |
初中 | 4500 | 30% |
高中 | 2000 | 50% |
为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,
则:(Ⅰ)样本容量为___________;(Ⅱ)抽取的高中生中,近视人数为___________.
 ,则
,则 =
=  集合
集合 ,则集合
,则集合 ( )
( ) C.
C. D.
D.
 中,直线l的参数方程:
中,直线l的参数方程: (t为参数),以直角坐标系的原点O为极点,x轴的非负半轴为极轴建立极坐标系,则以极点为圆心与直线l相切的圆的极坐标方程为 。
(t为参数),以直角坐标系的原点O为极点,x轴的非负半轴为极轴建立极坐标系,则以极点为圆心与直线l相切的圆的极坐标方程为 。
 在
在 处取得极值,则实数
处取得极值,则实数 的值是 .
的值是 .