题目内容
在正四面体ABCD（各棱都相等）中，E是BC的中点，则异面直线AE与CD所成的角的余弦值为 ．
【答案】分析：根据三角形的中位线平行于底边，作出异面直线所成的角，再解三角形求得即可．
解答：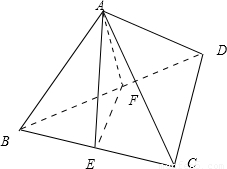
解：取BD的中点F，连接AF、EF，
∵E、F分别是BC、BD的中点，∴EF∥CD，
∴∠AEF为异面直线AE与CD所成的角，
设正四面体ABCD的棱长为2，则AE=AF=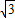
，EF=1，
在△AEF中，cos∠AEF=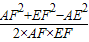
=
=
．
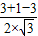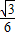故答案是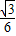
点评：本题考查异面直线所成的角．异面直线所成角的求法：1、作角（平行线）；2、证角（符合定义）；3、求角（解三角形）．
解答：
解：取BD的中点F，连接AF、EF，∵E、F分别是BC、BD的中点，∴EF∥CD，
∴∠AEF为异面直线AE与CD所成的角，
设正四面体ABCD的棱长为2，则AE=AF=
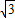，EF=1，在△AEF中，cos∠AEF=
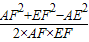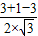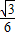==．故答案是
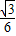
点评：本题考查异面直线所成的角．异面直线所成角的求法：1、作角（平行线）；2、证角（符合定义）；3、求角（解三角形）．
练习册系列答案
相关题目