题目内容

在正四面体ABCD中，其棱长为a，若正四面体ABCD有一个内切球，则这个球的表面积为
 
．
分析：作出正四面体的图形，球的球心位置，说明OE是内切球的半径，利用直角三角形，逐步求出内切球的表面积．
解答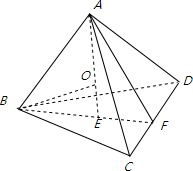：精英家教网解：如图O为正四面体ABCD的内切球的球心，正四面体的棱长为：a；
所以OE为内切球的半径，BF=AF=
3
a
2

BE=
3
a
3
，所以AE=
a2-(
3
a
3
)2
=
6
3
a，
BO2-OE2=BE2，
(
6
a
3
-OE)2-OE2=(
3
a
3
)2
所以 OE=
6
12
a
球的表面积为：4π•OE2=
a2π
6

故答案为：
a2π
6
点评：本题考查正四面体的内切球的表面积，是一道典型题目，考试常考题，考查空间想象能力，计算能力，是基础题．
练习册系列答案
相关题目
在正四面体ABCD中，E、F分别是BC、AD中点，则异面直线AE与CF所成的角是
 
．（用反三角值表示）
已知有关正三角形的一个结论：“在正三角形ABC中，若D是BC的中点，G是三角形ABC内切圆的圆心，则
AG
GD
=2”．若把该结论推广到正四面体（所有棱长均相等的三棱锥），则有结论：“在正四面体ABCD中，若M是正三角形BCD的中心，O是在正四面体ABCD内切球的球心，则
AO
OM
=
3
3
”．
某同学使用类比推理得到如下结论：
（1）同一平面内，三条不同的直线a，b，c，若a⊥c，b⊥c，则a∥b，类比出：空间中，三条不同的直线a，b，c，若a⊥c，b⊥c，则a∥b；
（2）a，b∈R，a-b＞0则a＞b，类比出：a，b∈C，a-b＞0则a＞b；
（3）以点（0，0）为圆心，r为半径的圆的方程是x2+y2=r2，类比出：以点（0，0，0）为球心，r为半径的球的方程是x2+y2+z2=r2；
（4）正三角形ABC中，M是BC的中点，O是△ABC外接圆的圆心，则
AO
OM
=2，类比出：在正四面体ABCD中，若M是△BCD的三边中线的交点，O为四面体ABCD外接球的球心，则
AO
OM
=3．
其中类比的结论正确的个数是（　　）
在正四面体ABCD中，点E为棱AD的中点，则异面直线AB与CE所成角的大小为
arccos
3
6
arccos
3
6
．
在正四面体ABCD中，E，F分别为BC，AD的中点，则异面直线AE与CF所成角的余弦值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网