题目内容
在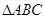 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
,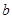 ,
,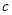 ,且
,且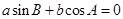 .
.
(1)求角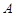 的大小;
的大小;
(2)若 ,
,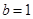 ,求
,求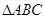 的面积.
的面积.
(1) ;(2)
;(2) .
.
解析试题分析:(1)首先利用正弦定理, ,
, ,代入方程,然后利用同角基本关系式,求出角
,代入方程,然后利用同角基本关系式,求出角 的大小;(2)利用余弦定理,
的大小;(2)利用余弦定理, ,得到关于
,得到关于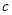 的方程,求出
的方程,求出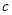 ,然后利用面积公式
,然后利用面积公式 ,得到答案.解三角形是高中重要的内容之一,正弦定理和余弦定理是两个重要的公式,等式里面达到边与角的统一,进行化简,还要结合面积公式,三角函数的化简问题,基本属于基础题型.
,得到答案.解三角形是高中重要的内容之一,正弦定理和余弦定理是两个重要的公式,等式里面达到边与角的统一,进行化简,还要结合面积公式,三角函数的化简问题,基本属于基础题型.
试题解析:(1)由 及正弦定理,得
及正弦定理,得  , 2分
, 2分 ,
, 
 , 4分
, 4分
 . 7分
. 7分
(2)解:由 ,
, ,
, 及余弦定理,得
及余弦定理,得 , 9分
, 9分
得 , 11分
, 11分 . 14分
. 14分
考点:1.正弦定理;2.余弦定理;3.面积公式.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
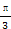 <C<
<C< 且
且 =
= .
. +
+ |=2,求
|=2,求 sin A)cos B=0.
sin A)cos B=0. ,b=
,b= ,求c;
,求c; 的取值范围.
的取值范围. -cos 2A=
-cos 2A= .
. ,b+c=3,求△ABC的面积.
,b+c=3,求△ABC的面积.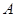 为
为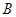 ,
, 的等差中项.
的等差中项.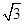 ,求b,c的值.
,求b,c的值. 中,角
中,角 所对的边分别为
所对的边分别为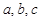 ,且
,且 ,
, ,求
,求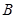 的取值范围.
的取值范围.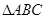 中,
中,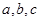 分别是内角
分别是内角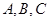 所对的边,且
所对的边,且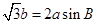 。
。 的大小;
的大小; 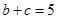 ,且
,且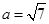 ,求
,求 的顶点
的顶点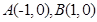 ,顶点
,顶点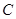 在直线
在直线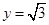 上;
上;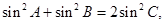 求点
求点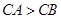 ,且
,且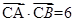 ,求角
,求角