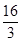题目内容
学校为扩大规模,把后山一块不规则的非农业用地规划建成一个矩形运动场地.已知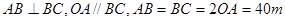 ,曲线段
,曲线段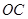 是以点
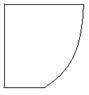
是以点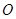 为顶点且开口向上的抛物线的一段(如图所示).如果要使矩形的相邻两边分别落在
为顶点且开口向上的抛物线的一段(如图所示).如果要使矩形的相邻两边分别落在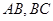 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段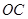 上,问应如何规划才能使运动场地面积最大?
上,问应如何规划才能使运动场地面积最大?

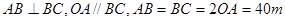 ,曲线段
,曲线段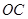 是以点
是以点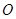 为顶点且开口向上的抛物线的一段(如图所示).如果要使矩形的相邻两边分别落在
为顶点且开口向上的抛物线的一段(如图所示).如果要使矩形的相邻两边分别落在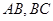 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段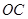 上,问应如何规划才能使运动场地面积最大?
上,问应如何规划才能使运动场地面积最大?

本试题主要是考查能合理建系,表示所求的面积,借助于函数的思想求解最值的运用。
解:建立平面直角坐标系如图所示,设曲线段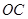 所在的抛物线方程为
所在的抛物线方程为 ……………………………………………………………………2分
……………………………………………………………………2分
由已知得点C的坐标为(20,40),代入方程得
 ………………………4分
………………………4分
设矩形运动场
 …………………6分
…………………6分

令 ……………8分
……………8分

 ………………………………………11分
………………………………………11分
 ………………12分
………………12分
解:建立平面直角坐标系如图所示,设曲线段
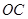 所在的抛物线方程为
所在的抛物线方程为 ……………………………………………………………………2分
……………………………………………………………………2分由已知得点C的坐标为(20,40),代入方程得

 ………………………4分
………………………4分设矩形运动场

 …………………6分
…………………6分
令
 ……………8分
……………8分
 ………………………………………11分
………………………………………11分 ………………12分
………………12分
练习册系列答案
相关题目
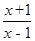 ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间; ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线 在点
在点 处切线的斜率为( )
处切线的斜率为( ) 

 在点(-1,-1)处的切线方程为
在点(-1,-1)处的切线方程为 在
在 处的切线平行于直线
处的切线平行于直线 ,则
,则


 ,若
,若 ,则
,则 ( )
( )



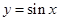 在
在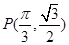 处的切线斜率是 .
处的切线斜率是 .
 ,则a的值是( )
,则a的值是( )