题目内容
(本题满分14分)
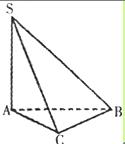
在多面体
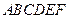 中,点
中,点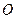 是矩形
是矩形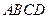 的对角线的交点,三角形
的对角线的交点,三角形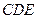 是等边三角形,棱
是等边三角形,棱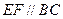 且
且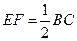 .
.(Ⅰ)证明:
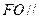 平面
平面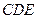 ;
;(Ⅱ)设
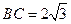 ,
,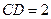 ,
, ,
,求
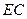 与平面
与平面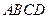 所成角的正弦值。
所成角的正弦值。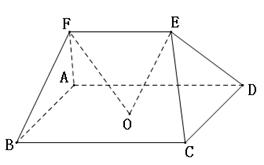
(Ⅰ)【证明】取CD中点M,连结OM.………………1分
在矩形ABCD中,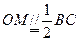 ,又
,又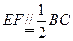 ,则
,则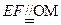 ,………………3分
,………………3分
连结EM,于是四边形EFOM为平行四边形.
∴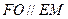 ………………5分
………………5分
又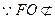 平面CDE,且EM
平面CDE,且EM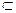 平面CDE,
平面CDE,
∴FO∥平面CDE ………………6分
(Ⅱ)连结FM,由(Ⅰ)和已知条件,在等边△CDE中,
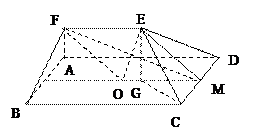
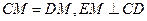 且
且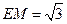 ,又
,又 .
.
因此平行四边形EFOM为菱形,………………8分
过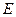 作
作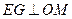 于
于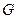
∵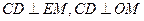 ,
,
∴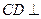 平面
平面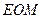 ,∴
,∴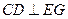
因此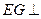 平面
平面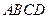
所以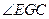 为
为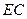 与底面
与底面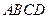 所成角………………10分
所成角………………10分
在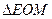 中
中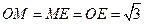 , 则
, 则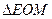 为正三角形。
为正三角形。
∴点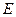 到平面
到平面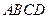 的距离为
的距离为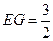 ,………………12分
,………………12分
所以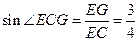
即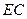 与平面
与平面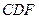 所成角的正弦值为
所成角的正弦值为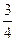 。………………14分
。………………14分
在矩形ABCD中,
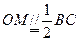 ,又
,又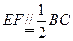 ,则
,则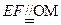 ,………………3分
,………………3分连结EM,于是四边形EFOM为平行四边形.
∴
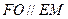 ………………5分
………………5分又
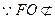 平面CDE,且EM
平面CDE,且EM 平面CDE,
平面CDE,∴FO∥平面CDE ………………6分
(Ⅱ)连结FM,由(Ⅰ)和已知条件,在等边△CDE中,
 且
且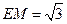 ,又
,又 .
.因此平行四边形EFOM为菱形,………………8分
过
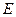 作
作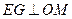 于
于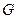
∵
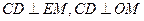 ,
,∴
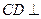 平面
平面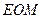 ,∴
,∴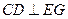
因此
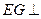 平面
平面
所以
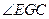 为
为 与底面
与底面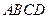 所成角………………10分
所成角………………10分在
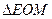 中
中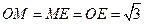 , 则
, 则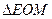 为正三角形。
为正三角形。∴点
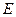 到平面
到平面 的距离为
的距离为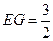 ,………………12分
,………………12分所以
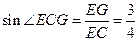
即
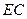 与平面
与平面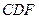 所成角的正弦值为
所成角的正弦值为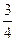 。………………14分
。………………14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,M、N、P、Q分别为AD、CD、
中,M、N、P、Q分别为AD、CD、 、
、 的中点.
的中点.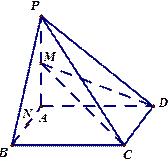
 中,
中, ,平面
,平面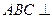 平面
平面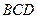 ,
,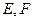 分别为棱
分别为棱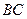 和
和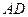 的中点。
的中点。
 平面
平面 ;
;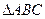 内的点
内的点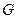 满足
满足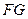 ∥平面
∥平面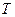 ,试描述点集
,试描述点集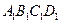 ,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.
,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.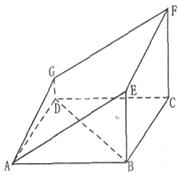

 )如图,棱锥
)如图,棱锥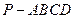 的底面
的底面 是矩形,
是矩形,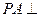 面
面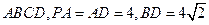 ,
,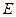 为
为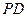 的中点.
的中点.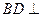 面
面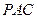 ;
; 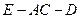 的余弦值;
的余弦值;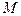 为
为 的中点,在棱
的中点,在棱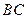 上是否存在点
上是否存在点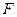 ,
,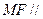 面
面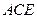 ?如果存在,请指出
?如果存在,请指出 点的位置;
点的位置;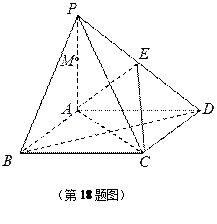
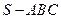 中,
中,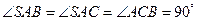 ,且
,且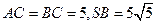 。
。
 ;
;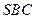 与底面
与底面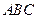 所成二面角的大小;
所成二面角的大小; 如图,正方形
如图,正方形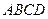 所在平面与
所在平面与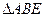 所在平面垂直,
所在平面垂直,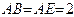 ,
,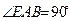 ,
,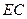 中点为
中点为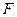 .
.
 与平面
与平面 所成角
所成角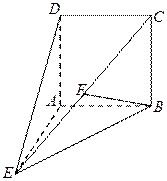
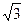 ,两个平面分别截球面得到两个圆⊙O1与⊙O2,若
,两个平面分别截球面得到两个圆⊙O1与⊙O2,若