题目内容
如图O是△ABC内的一点，且
+k•
+t•
=
，（k，t∈R）
（Ⅰ）若O是△ABC的重心，写出k，t的值；
（Ⅱ）若O是△ABC的外心，且k=
，t=
，求cos∠AOB的值；
（Ⅲ）若O是△ABC的外心，且AB=2，AC=3，求
•
的值．
| OA |
| OB |
| OC |
| 0 |
（Ⅰ）若O是△ABC的重心，写出k，t的值；
（Ⅱ）若O是△ABC的外心，且k=
| 3 |
| 6 |
（Ⅲ）若O是△ABC的外心，且AB=2，AC=3，求
| OA |
| BC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（Ⅰ）因为O是△ABC的重心，所以k=t=1；
（Ⅱ）若O是△ABC的外心，则|
|=|
|=|
|，又因为
+
+
=
，所以
+
=-
，两边平方即可求出cos∠AOB的值；
（Ⅲ）取BC中点为D，连接OD，AD，因为O为△ABC的外心，所以OD⊥BC，进而求出
•
的值即可．
（Ⅱ）若O是△ABC的外心，则|
| OA |
| OB |
| OC |
| OA |
| 3 |
| OB |
| 6 |
| OC |
| O |
| OA |
| 3 |
| OB |
| 6 |
| OC |
（Ⅲ）取BC中点为D，连接OD，AD，因为O为△ABC的外心，所以OD⊥BC，进而求出
| OA |
| BC |
解答：
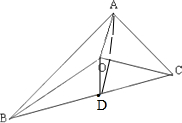解：（Ⅰ）因为O是△ABC的重心，
所以k=t=1；
（Ⅱ）若O是△ABC的外心，
则|
|=|
|=|
|，
又因为
+
+
=
，
所以
+
=-
，
两边平方可得，1+3+2
cos∠AOB=6，
即cos∠AOB=
；
（Ⅲ）取BC中点为D，连接OD，AD，
因为O为△ABC的外心，
所以OD⊥BC，
•
=（
+
）•
=
•
=-
（
+
）•（
-
）
=-
（
2-
2）
=-
．
解：（Ⅰ）因为O是△ABC的重心，所以k=t=1；
（Ⅱ）若O是△ABC的外心，
则|
| OA |
| OB |
| OC |
又因为
| OA |
| 3 |
| OB |
| 6 |
| OC |
| O |
所以
| OA |
| 3 |
| OB |
| 6 |
| OC |
两边平方可得，1+3+2
| 3 |
即cos∠AOB=
| ||
| 3 |
（Ⅲ）取BC中点为D，连接OD，AD，
因为O为△ABC的外心，
所以OD⊥BC，
| OA |
| BC |
| OD |
| DA |
| BC |
| DA |
| BC |
=-
| 1 |
| 2 |
| AB |
| AC |
| AC |
| AB |
=-
| 1 |
| 2 |
| AC |
| AB |
=-
| 5 |
| 2 |
点评：本题主要考查了平面向量数量积的定义以及性质的应用，考查了平面向量数量积的运算，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=
．若f（-a）+f（a）≤0，则a的取值范围是（ ）
|
| A、[-1，1] |
| B、[-2，0] |
| C、[0，2] |
| D、[-2，2] |
如图，E是以AB为直径的半圆上异于A、B的点，矩形ABCD所在的平面垂直于该半圆所在的平面，且AB=2AD=2．
一个被绳子牵着的小球做圆周运动（如图）．它从初始位置P0开始，按逆时针方向以角速度ω rad/s做圆周运动．已知绳子的长度为l，求：