题目内容
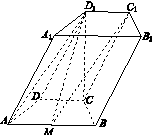
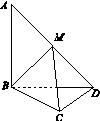
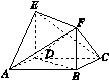
如图13所示,在四棱柱ABCD A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.

图13
(1)求证:C1M∥平面A1ADD1;
(2)若CD1垂直于平面ABCD且CD1= ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
解:(1)证明:因为四边形ABCD是等腰梯形,
且AB=2CD,所以AB∥DC,
又M是AB的中点,
所以CD∥MA且CD=MA.
连接AD1.因为在四棱柱ABCD A1B1C1D1中,
CD∥C1D1,CD=C1D1,
所以C1D1∥MA,C1D1=MA,
所以四边形AMC1D1为平行四边形,
因此,C1M∥D1A.
又C1M⊄平面A1ADD1,D1A⊂平面A1ADD1,
所以C1M∥平面A1ADD1.
(2)方法一:连接AC,MC.
由(1)知,CD∥AM且CD=AM,
所以四边形AMCD为平行四边形,
所以BC=AD=MC.
由题意∠ABC=∠DAB=60°,
所以△MBC为正三角形,
因此AB=2BC=2,CA= ,
,
因此CA⊥CB.
设C为坐标原点,建立如图所示的空间直角坐标系C xyz.

所以A( ,0,0),B(0,1,0),D1(0,0,
,0,0),B(0,1,0),D1(0,0, ).
).
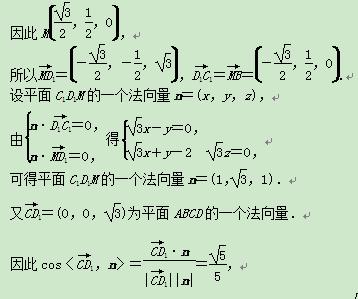 所以平面C1D1M和平面ABCD所成的角(锐角)的余弦值为
所以平面C1D1M和平面ABCD所成的角(锐角)的余弦值为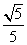 .
.
方法二:由(1)知,平面D1C1M∩平面ABCD=AB,点过C向AB引垂线交AB于点N,连接D1N.
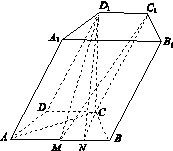
由CD1⊥平面ABCD,可得D1N⊥AB,
因此∠D1NC为二面角C1 AB C的平面角.
在Rt△BNC中,BC=1,∠NBC=60°,
可得CN= ,
,
所以ND1= =
=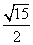 .
.
在Rt△D1CN中,cos∠D1NC=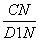 =
=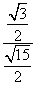 =
=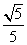 ,
,
所以平面C1D1M和平面ABCD所成的角(锐角)的余弦值为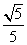 .
.

练习册系列答案
相关题目
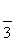 ,M为BC上一点,且BM=
,M为BC上一点,且BM= ,MP⊥AP.
,MP⊥AP.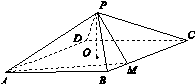
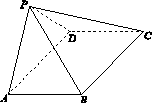
 ,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.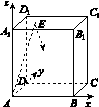
 .
.
 ;
;