题目内容
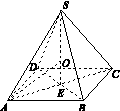
已知如图G78所示的多面体中,四边形ABCD是菱形,四边形BDEF是矩形,ED⊥平面ABCD,∠BAD= .
.
(1)求证:平面BCF∥平面AED;
(2)若BF=BD=a,求四棱锥ABDEF的体积.
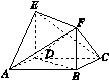
图G78
解:(1)证明:∵四边形ABCD是菱形,
∴BC∥AD.
∵BC⊄平面ADE,AD⊂平面AED,
∴BC∥平面ADE.
又∵四边形BDEF是矩形,∴BF∥DE.
∵BF⊄平面ADE,DE⊂平面ADE,
∴BF∥平面ADE.
∵BC⊂平面BCF,BF⊂平面BCF,且BC∩BF=B,
∴平面BCF∥平面AED.
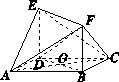
(2)如图,连接AC,AC∩BD=O.
∵四边形ABCD是菱形,
∴AC⊥BD.
又∵ED⊥平面ABCD,AC⊂平面ABCD,∴ED⊥AC.
∵ED,BD⊂平面BDEF,且ED∩BD=D,
∴AC⊥平面BDEF,
∴AO为四棱锥ABDEF的高.
又∵四边形ABCD是菱形,∠BAD= ,
,
∴△ABD为等边三角形.
又∵BF=BD=a,
∴AD=a,AO= a,
a,
∴S四边形BDEF=a2,∴V四棱锥ABDEF=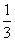 ·a2·
·a2· a=
a= a3.
a3.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
下列4个表格中,可以作为离散型随机变量分布列的一个是( )
A.
| X | 0 | 1 | 2 |
| P | 0.3 | 0.4 | 0.5 |
B.
| X | 0 | 1 | 2 |
| P | 0.3 | -0.1 | 0.8 |
C.
| X | 1 | 2 | 3 | 4 |
| P | 0.2 | 0.5 | 0.3 | 0 |
D.
| X | 0 | 1 | 2 |
| P |
|
|
|
 ,E(ξ)=1,则D(ξ)=________.
,E(ξ)=1,则D(ξ)=________. B.16π C.9π D.
B.16π C.9π D.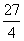

 ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.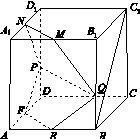
 B.
B.
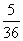 D.
D.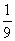



 B.
B.  C.
C.  D.
D. 