题目内容
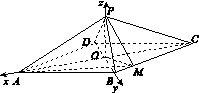
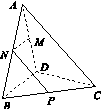
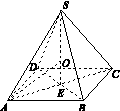
如图13所示,四棱锥PABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=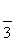 ,M为BC上一点,且BM=
,M为BC上一点,且BM= ,MP⊥AP.
,MP⊥AP.
(1)求PO的长;
(2)求二面角APMC的正弦值.
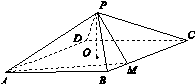
图13
解:(1)如图所示,连接AC,BD,因为四边形ABCD为菱形,所以AC∩ BD=O,且AC⊥BD.以O为坐标原点,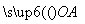 ,
,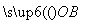 ,
, 的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系O xyz.
的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系O xyz.
因为∠BAD=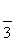 ,
,
所以OA=AB·cos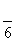 =
= ,OB=AB·sin
,OB=AB·sin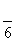 =1,
=1,
所以O(0,0,0),A( ,0,0),B(0,1,0),C(-
,0,0),B(0,1,0),C(- ,0,0),
,0,0),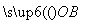 =(0,1,0),
=(0,1,0),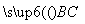 =(-
=(- ,-1,0).
,-1,0).
由BM= ,BC=2知,
,BC=2知,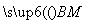 =
=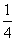
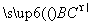 =
=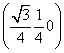 ,
,
从而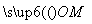 =
=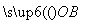 +
+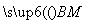 =
= ,
,
即M .
.
设P(0,0,a),a>0,则 =(-
=(- ,0,a),
,0,a),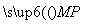 =
= .因为MP⊥AP,所以
.因为MP⊥AP,所以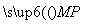 ·
· =0,即-
=0,即-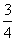 +a2=0,所以a=
+a2=0,所以a= 或a=-
或a=- (舍去),即PO=
(舍去),即PO= .
.
(2)由(1)知, =
=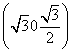 ,
,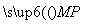 =
= ,
,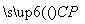 =
=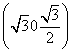 .设平面APM的法向量为n1=(x1,y1,z1),平面PMC的法向量为n2=(x2,y2,z2).
.设平面APM的法向量为n1=(x1,y1,z1),平面PMC的法向量为n2=(x2,y2,z2).
由n1· =0, n1·
=0, n1·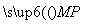 =0,得
=0,得
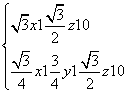 故可取n1=
故可取n1= .
.
由n2·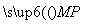 =0,n2·
=0,n2·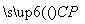 =0,得
=0,得
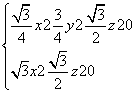 故可取n2=(1,-
故可取n2=(1,- ,-2).
,-2).
从而法向量n1,n2的夹角的余弦值为
cos〈n1,n2〉=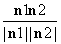 =-
=-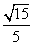 ,
,
故所求二面角APMC的正弦值为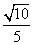 .
.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 +
+ =1表示焦点在x轴上且离心率小于
=1表示焦点在x轴上且离心率小于 的椭圆的概率为( )
的椭圆的概率为( ) B.
B. C.
C. D.
D.

 B.16π C.9π D.
B.16π C.9π D.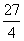
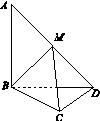

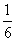 B.
B.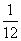
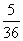 D.
D.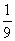
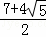 π B. (12+4
π B. (12+4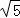 )π C.
)π C. 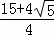 π D. (13+4
π D. (13+4