题目内容
(本小题满分13分)
如图,在正四面体 中,
中, 分别是棱
分别是棱 的中点.
的中点.

(1)求证:四边形 是平行四边形;
是平行四边形;
(2)求证: 平面
平面 ;
;
(3)求证: 平面
平面 .
.
见解析.
【解析】
试题分析:第一问应用三角形的中位线的性质,可知四边形的一组对边平行且相等的,从而根据平行四边形的判定定理,得出结果,对于第二问,注意把握线面平行的判定定理的内容,找准平行线即可,三角形的中位线是现成的,对于第三问,掌握线面垂直的判定定理的内容,找准两条相交直线与之垂直即可,正三角形的中线和垂线是重合的,好好写即可.
试题解析:
证明:(1)∵ 分别是棱
分别是棱 的中点,
的中点,
∴ ,且
,且 , (2分)
, (2分)
∴ 且
且 , (3分)
, (3分)
∴四边形 是平行四边形. (4分)
是平行四边形. (4分)
(2)由(1)知, , (5分)
, (5分)
且 平面
平面 ,
, 平面
平面 , (7分)
, (7分)
∴ 平面
平面 . (8分)
. (8分)
(3)∵ 是正四面体,
是正四面体,
所以它的四个面是全等的等边三角形. (9分)

∵ H是BC的中点,
∴ . (11分)
. (11分)
又SH平面SAH,AH平面SAH,且 ,(12分)
,(12分)
∴ 平面
平面 . (13分)
. (13分)
考点:平行四边形的判定,线面平行的判定,线面垂直的判定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 与
与
 与
与
 与
与
 与
与
 ,
, 有零点,则m的取值范围是
有零点,则m的取值范围是



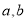 与平面
与平面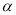 ,则下列四个命题中假命题是
,则下列四个命题中假命题是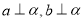 ,那么
,那么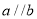 B.如果
B.如果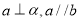 ,那么
,那么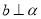
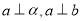 ,那么
,那么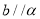 D.如果
D.如果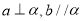 ,那么
,那么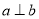
 的焦点坐标是
的焦点坐标是 B.
B. C.
C. D.
D.
 且与
且与 有相同焦点的椭圆的方程是 .
有相同焦点的椭圆的方程是 . 的倾斜角为135;命题q:直角坐标平面内的三点A(-1,-3),B(1,1),C(2,2)共线. 则下列判断正确的是
的倾斜角为135;命题q:直角坐标平面内的三点A(-1,-3),B(1,1),C(2,2)共线. 则下列判断正确的是 为假 B.
为假 B. 为真 C.
为真 C. 为真 D.
为真 D. 为真
为真 在点
在点 处的切线方程是( )
处的切线方程是( ) B.
B.
 D.
D.
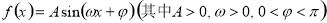 在
在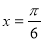 处取得最大值3,其相邻两条对称轴间的距离为
处取得最大值3,其相邻两条对称轴间的距离为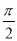 .
.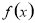 的解析式;
的解析式;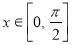 ,求
,求