题目内容
17.设z1=2x+1+(x2-3x+2)i,z2=x2-2+(x2+x-6)i(x∈R).(1)若z1是纯虚数,求实数x的取值范围;
(2)若z1>z2,求实数x的取值范围.
分析 (1)利用复数的基本概念,列出方程求解即可.
(2)解法一.利用复数是实数求出x的值,然后判断即可.
解法二:利用复数是实数以及不等式列出混合组,判断求解即可.
解答 解:(1)依题意得$\left\{{\begin{array}{l}{2x+1=0}\\{{x^2}-3x+2≠0}\end{array}}\right.$---------------------(2分)
$⇒\left\{{\begin{array}{l}{x=-\frac{1}{2}}\\{(x-1)(x-2)≠0}\end{array}}\right.⇒\left\{{\begin{array}{l}{x=-\frac{1}{2}}\\{x≠1且x≠2}\end{array}}\right.$----------------------(4分)$⇒x=-\frac{1}{2}$
所以实数x的取值范围是$x=-\frac{1}{2}$----------------------(6分)
(2)解一、依题意得$\left\{{\begin{array}{l}{{x^2}-3x+2=0}\\{{x^2}+x-6=0}\end{array}}\right.$-------------------(8分)$⇒\left\{{\begin{array}{l}{(x-1)(x-2)=0}\\{(x+3)(x-2)=0}\end{array}}\right.⇒\left\{{\begin{array}{l}{x=1或x=2}\\{x=-3或x=2}\end{array}}\right.$
所以x=2----------------------(10分)
检验:当x=2时,${z_1}=2×2+1=5,{z_2}={2^2}-2=2$,满足z1>z2符合题意.
所以实数x的取值范围是x=2----------------------------(12分)
解二、依题意得$\left\{{\begin{array}{l}{{x^2}+x-6=0}\\{{x^2}-3x+2=0}\\{2x+1>{x^2}-2}\end{array}}\right.$-------------------(9分)$\begin{array}{l}\\⇒\left\{{\begin{array}{l}{(x+3)(x-2)=0}\\{(x-1)(x-2)=0}\\{(x-3)(x+1)<0}\end{array}}\right.⇒\left\{{\begin{array}{l}{x=-3或x=2}\\{x=1或x=2}\\{-1<x<3}\end{array}⇒x=2}\right.\end{array}$
所以实数x的取值范围是x=2-------------------(12分)
点评 本题考查复数的基本运算,复数的基本概念,是基础题.

| A. | $-\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
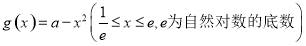 与
与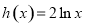 的图象上存在关于
的图象上存在关于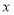 轴对称的点,则实数
轴对称的点,则实数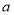 的取值范围是( )
的取值范围是( )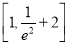 B.
B.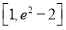
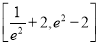 D.
D.