题目内容
求过点(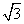 ,-
,-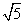 ),且与椭圆
),且与椭圆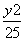 +
+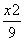 =1有相同焦点的椭圆的标准方程.
=1有相同焦点的椭圆的标准方程.
解 法一 椭圆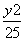 +
+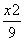 =1的焦点为(0,-4),(0,4),即c=4.由椭圆的定义知,
=1的焦点为(0,-4),(0,4),即c=4.由椭圆的定义知,
2a=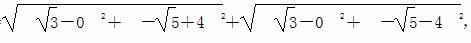
解得a=2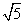 .由c2=a2-b2可得b2=4.
.由c2=a2-b2可得b2=4.
所以所求椭圆的标准方程为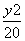 +
+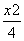 =1.
=1.
法二 因为所求椭圆与椭圆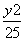 +
+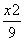 =1的焦点相同,所以其焦点在y轴上,且c2=25-9=16.
=1的焦点相同,所以其焦点在y轴上,且c2=25-9=16.
设它的标准方程为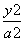 +
+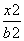 =1(a>b>0).
=1(a>b>0).
因为c2=16,且c2=a2-b2,故a2-b2=16.①
又点(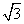 ,-
,-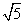 )在所求椭圆上,
)在所求椭圆上,
所以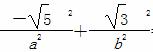 =1,即
=1,即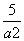 +
+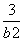 =1.②
=1.②
由①②得b2=4,a2=20,
所以所求椭圆的标准方程为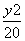 +
+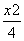 =1.
=1.
规律方法 (1)一般地,解决与到焦点的距离有关问题时,首先应考虑用定义来解决.
(2)求椭圆的标准方程有两种方法
①定义法:根据椭圆的定义,确定a2,b2的值,结合焦点位置可写出椭圆方程.
②待定系数法:若焦点位置明确,则可设出椭圆的标准方程,结合已知条件求出a,b;若焦点位置不明确,则需要分焦点在x轴上和y轴上两种情况讨论,也可设椭圆的方程为Ax2+By2=1(A>0,B>0,A≠B).

练习册系列答案
相关题目
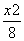 +
+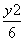 =1 B.
=1 B.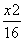 +
+ =1 D.
=1 D.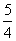 ;
;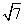 )和Q(-6
)和Q(-6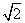 ,-7).
,-7).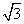 B.
B.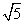 C.2 D.
C.2 D.