题目内容
根据下列条件,求双曲线的标准方程.
(1)虚轴长为12,离心率为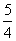 ;
;
(2)焦距为26,且经过点M(0,12).
(3)经过两点P(-3,2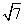 )和Q(-6
)和Q(-6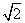 ,-7).
,-7).
解 (1)设双曲线的标准方程为
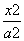 -
-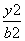 =1或
=1或 -
- =1(a>0,b>0).
=1(a>0,b>0).
由题意知,2b=12,e= =
=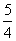 .∴b=6,c=10,a=8.
.∴b=6,c=10,a=8.
∴双曲线的标准方程为 -
- =1或
=1或 -
- =1.
=1.
(2)∵双曲线经过点M(0,12),∴M(0,12)为双曲线的一个顶点,故焦点在y轴上,且a=12.
又2c=26,∴c=13.∴b2=c2-a2=25.
∴双曲线的标准方程为 -
-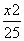 =1.
=1.
(3)设双曲线方程为mx2-ny2=1(mn>0).
∴
∴双曲线的标准方程为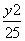 -
- =1.
=1.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
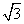 ,-
,-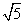 ),且与椭圆
),且与椭圆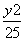 +
+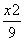 =1有相同焦点的椭圆的标准方程.
=1有相同焦点的椭圆的标准方程.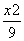 -
-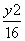 =1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△ PQF的周长为________.
=1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△ PQF的周长为________.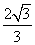 B.
B.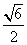 C.
C.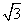
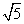 ,0),则其离心率为________.
,0),则其离心率为________. ,|AF|<|BF|,则|AF|=________.
,|AF|<|BF|,则|AF|=________. -
- =1(a>0)的焦点为(5,0),则该双曲线的离心率等于( ).
=1(a>0)的焦点为(5,0),则该双曲线的离心率等于( ). B.
B.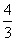 C.
C. D.
D.