题目内容
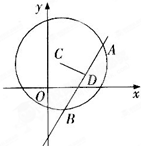
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.
(1)求证:无论m为何值,直线L与圆C恒有两个公共点;
(2)当m为何值时,直线被圆截得的弦最短,最短的弦长是多少?
(1)求证:无论m为何值,直线L与圆C恒有两个公共点;
(2)当m为何值时,直线被圆截得的弦最短,最短的弦长是多少?
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:(1)通过直线l转化为直线系,求出直线恒过的定点;
(2)说明直线l被圆C截得的弦长最小时,圆心与定点连线与直线l垂直,求出斜率即可求出m的值,再由勾股定理即可得到最短弦长.
(2)说明直线l被圆C截得的弦长最小时,圆心与定点连线与直线l垂直,求出斜率即可求出m的值,再由勾股定理即可得到最短弦长.
解答:
 (1)证明:将l的方程整理为(x+y-4)+m(2x+y-7)=0,
(1)证明:将l的方程整理为(x+y-4)+m(2x+y-7)=0,
由
,解得x=3,y=1,
则无论m为何值,直线l过定点D(3,1).
(2)解:因为(3-1)2+(1-2)2=5<25,
则点D在圆C的内部,直线l与圆C相交.
圆心C(1,2),半径为5,|CD|=
=
,
当截得的弦长最小时,l⊥CD,由于kCD=
=-
,
则l的斜率为2,即有-
=2,解得m=-
.
此时最短弦长为2
=4
,
故当m=-
时,直线被圆截得的弦最短,最短的弦长是4
.
 (1)证明:将l的方程整理为(x+y-4)+m(2x+y-7)=0,
(1)证明:将l的方程整理为(x+y-4)+m(2x+y-7)=0,由
|
则无论m为何值,直线l过定点D(3,1).
(2)解:因为(3-1)2+(1-2)2=5<25,
则点D在圆C的内部,直线l与圆C相交.
圆心C(1,2),半径为5,|CD|=
| (3-1)2+(1-2)2 |
| 5 |
当截得的弦长最小时,l⊥CD,由于kCD=
| 2-1 |
| 1-3 |
| 1 |
| 2 |
则l的斜率为2,即有-
| 2m+1 |
| m+1 |
| 3 |
| 4 |
此时最短弦长为2
| 52-5 |
| 5 |
故当m=-
| 3 |
| 4 |
| 5 |
点评:本题考查直线系方程的应用,考查直线与圆的位置关系,考查平面几何知识的运用,考查计算能力,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
在△ABC中,D在BC上,
=2
,设
=
,
=
,则
=( )
| BD |
| DC |
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
对于在区间[a,b]上有意义的两个函数f(x)和g(x),如果对于任意x∈[a,b]均有|f(x)-g(x)|≤1成立,则称函数f(x)和g(x)在区间[a,b]上是接近的.若f(x)=log2(ax+1)与g(x)=log2x在区[1,2]上是接近的,则实数a的取值范围是( )
| A、?[0,1] |
| B、[2,3] |
| C、[0,2) |
| D、(1,4) |
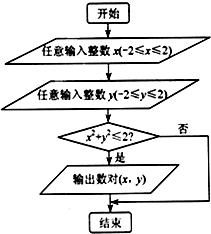 执行如图的程序框图,任意输入一次x(x∈Z,-2≤x≤2)与y(y∈Z,-2≤y≤2),则能输出数对(x,y)的概率为( )
执行如图的程序框图,任意输入一次x(x∈Z,-2≤x≤2)与y(y∈Z,-2≤y≤2),则能输出数对(x,y)的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知p:“a=b”是“ac=bc”充要条件;q:“a<5”是“a<3”的必要不充分条件,则下列判断中,错误的是( )
| A、p或q为真,非q为假 |
| B、p或q为真,非p为真 |
| C、p且q为假,非p为假 |
| D、p且q为假,p或q为真 |