题目内容
12.设平面向$\overline{a}$=(sinx,cosx),$\overrightarrow{b}$=($\sqrt{3}$,-1).(1)若$\overrightarrow{a}$⊥$\overrightarrow{b}$,求tan(2x+$\frac{π}{4}$)的值;
(2)若x∈[0,π],求|$\overrightarrow{a}-\overrightarrow{b}$|的取值范围.
分析 (1)令$\overrightarrow{a}•\overrightarrow{b}=0$解出x,再计算tan(2x+$\frac{π}{4}$)的值;
(2)求出$\overrightarrow{a}-\overrightarrow{b}$的坐标,计算($\overrightarrow{a}-\overrightarrow{b}$)2,根据x的范围利用三角函数的性质得出|$\overrightarrow{a}-\overrightarrow{b}$|的取值范围.
解答 解:(1)∵$\overrightarrow{a}⊥\overrightarrow{b}$,∴$\overrightarrow{a}•\overrightarrow{b}=0$,即$\sqrt{3}$sinx-cosx=0,
∴tanx=$\frac{\sqrt{3}}{3}$.∴x=$\frac{π}{6}+kπ$.
∴tan(2x+$\frac{π}{4}$)=tan($\frac{7π}{12}$+2kπ)=tan$\frac{7π}{12}$=tan($\frac{π}{3}+\frac{π}{4}$)=$\frac{tan\frac{π}{3}+tan\frac{π}{4}}{1-tan\frac{π}{3}tan\frac{π}{4}}$=$\frac{\sqrt{3}+1}{1-\sqrt{3}}$=-2-$\sqrt{3}$.
(2)$\overrightarrow{a}-\overrightarrow{b}$=(sinx-$\sqrt{3}$,cosx+1),
∴($\overrightarrow{a}-\overrightarrow{b}$)2=(sinx-$\sqrt{3}$)2+(cosx+1)2=-2$\sqrt{3}$sinx+2cosx+5=4cos(x+$\frac{π}{3}$)+5.
∵x∈[0,π],∴x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$].
∴当x+$\frac{π}{3}$=$\frac{π}{3}$时,($\overrightarrow{a}-\overrightarrow{b}$)2取得最大值7,当x+$\frac{π}{3}$=π时,($\overrightarrow{a}-\overrightarrow{b}$)2取得最小值1.
∴|$\overrightarrow{a}-\overrightarrow{b}$|的取值范围是[1,$\sqrt{7}$].
点评 本题考查了平面向量的数量积运算,三角函数的图象与性质,属于中档题.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | -1 | B. | 1 | C. | ±1 | D. | 0 |
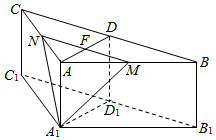 如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.
如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.