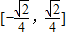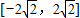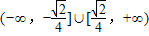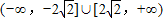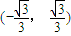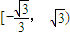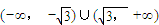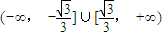题目内容
若过点A(0,-1)的直线与曲线x2+(y-2)2=1有公共点,则直线l的斜率的取值范围为( )
A、[-
| ||||||||
B、[-2
| ||||||||
C、(-∞,-
| ||||||||
D、(-∞,-2
|
分析:设直线l的斜率为k,得到其方程,再由直线与曲线x2+(y-2)2=1有公共点,即圆心到直线的距离小于或等于半径求解.
解答:解:设直线l的斜率为k,其方程为:kx-y-1=0
∵直线与曲线x2+(y-2)2=1有公共点
∴圆心到直线的距离小于或等于半径
∴d=
≤1
∴k≥2
或k≤-2
故选D
∵直线与曲线x2+(y-2)2=1有公共点
∴圆心到直线的距离小于或等于半径
∴d=
| 3 | ||
|
∴k≥2
| 2 |
| 2 |
故选D
点评:本题主要考查直线与圆的位置关系,处理方法要侧重于几何法,即“R,d”法.当R<d时直线与圆相离,当R>d时直线与圆相交,当R=d时直线与圆相切.

练习册系列答案
相关题目
若过点A(0,-1)的直线l与曲线x2+(y-3)2=12有公共点,则直线l的斜率的取值范围为( )
A、(-
| ||||||||
B、[-
| ||||||||
C、(-∞, -
| ||||||||
D、(-∞, -
|
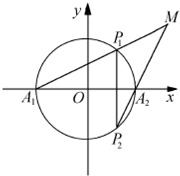 如图,A1、A2为圆x2+y2=1与x轴的两个交点,P1P2为垂直于x轴的弦,且A1P1与A2P2的交点为M.
如图,A1、A2为圆x2+y2=1与x轴的两个交点,P1P2为垂直于x轴的弦,且A1P1与A2P2的交点为M.