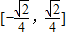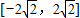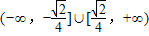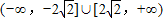题目内容
若过点A(0,-1)的直线l与曲线x2+(y-3)2=12有公共点,则直线l的斜率的取值范围为( )A.
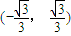
B.
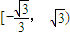
C.
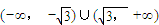
D.
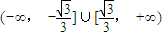
【答案】分析:当直线l的斜率存在时,由直线l过已知点A,写出直线l的方程,然后由圆的方程找出圆心坐标和圆的半径,因为直线l与圆有公共点,所以圆心到直线的距离小于等于圆的半径,利用点到直线的距离公式列出关于k的不等式,求出不等式的解集即可得到直线l的斜率k的取值范围.
解答:解:当直线l的斜率存在时,设直线l的斜率为k,由直线l过(0,-1),
得到直线l的方程为:y+1=kx,即kx-y-1=0,
由圆的方程找出圆心坐标为(0,3),圆的半径r=2 ,
,
因为直线l与圆有公共点,所以圆心到直线l的距离d= ≤r=2
≤r=2 ,
,
化简得:(k+ )(k-
)(k- )≥0,可化为:
)≥0,可化为:
 或
或 ,解得:k≥
,解得:k≥ 或k≤-
或k≤- ,
,
则直线l的斜率的取值范围为(-∞,- ]∪[
]∪[ ,+∞).
,+∞).
故选D
点评:此题考查学生掌握直线与圆有公共点时所满足的条件,灵活运用点到直线的距离公式化简求值,是一道中档题.
解答:解:当直线l的斜率存在时,设直线l的斜率为k,由直线l过(0,-1),
得到直线l的方程为:y+1=kx,即kx-y-1=0,
由圆的方程找出圆心坐标为(0,3),圆的半径r=2
 ,
,因为直线l与圆有公共点,所以圆心到直线l的距离d=
 ≤r=2
≤r=2 ,
,化简得:(k+
 )(k-
)(k- )≥0,可化为:
)≥0,可化为: 或
或 ,解得:k≥
,解得:k≥ 或k≤-
或k≤- ,
,则直线l的斜率的取值范围为(-∞,-
 ]∪[
]∪[ ,+∞).
,+∞).故选D
点评:此题考查学生掌握直线与圆有公共点时所满足的条件,灵活运用点到直线的距离公式化简求值,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若过点A(0,-1)的直线与曲线x2+(y-2)2=1有公共点,则直线l的斜率的取值范围为( )
A、[-
| ||||||||
B、[-2
| ||||||||
C、(-∞,-
| ||||||||
D、(-∞,-2
|
若过点A(0,-1)的直线l与曲线x2+(y-3)2=12有公共点,则直线l的斜率的取值范围为( )
A、(-
| ||||||||
B、[-
| ||||||||
C、(-∞, -
| ||||||||
D、(-∞, -
|
 如图,A1、A2为圆x2+y2=1与x轴的两个交点,P1P2为垂直于x轴的弦,且A1P1与A2P2的交点为M.
如图,A1、A2为圆x2+y2=1与x轴的两个交点,P1P2为垂直于x轴的弦,且A1P1与A2P2的交点为M.