题目内容
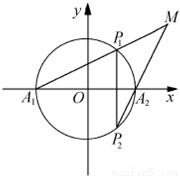
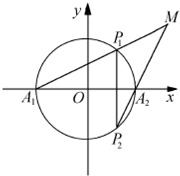如图，A1、A2为圆x2+y2=1与x轴的两个交点，P1P2为垂直于x轴的弦，且A1P1与A2P2的交点为M．（1）求动点M的轨迹方程；
（2）记动点M的轨迹为曲线E，若过点A（0，1）的直线l与曲线E交于y轴右边不同两点C、B，且
| AC |
| AB |
分析：（1）直线A1P1：y=
•(x+1)，直线A2P2：y=
，由M是A1P1和A2P2的交点，求得xm=
，xp=
，而yp=
=
，由此能够导出M点轨迹方程．
（2）设直线l方程为y=kx+1，x2-（kx+1）2=1，xc=
，xb=
，由
=2
，得k2=
，从而得到直线l方程．
| yp |
| xp+1 |
| 1-xp |
| x-1 |
| 1 |
| xp |
| 1 |
| xm |
| 1-xp2 |
| ||
| xm |
（2）设直线l方程为y=kx+1，x2-（kx+1）2=1，xc=
-k+
| ||
| k2-1 |
-k-
| ||
| k2-1 |
| AC |
| AB |
| 9 |
| 5 |
解答：解：（1）直线A1P1：y=
•(x+1)，直线A2P2：y=
，
∵M是A1P1和A2P2的交点，所以
•(xm+1)=
•(xm-1)，
求得xm=
，xp=
，
而yp=
=
，
所以M点轨迹方程是x2-y2=1．
（2）设直线l方程为y=kx+1，
∴x2-（kx+1）2=1，
xc=
，
xb=
，
∵
=2
，，所以xc=2xb，
将上面式子代入，解得k2=
，
因为直线l与曲线E交于y轴“右边”不同两点C，B，
所以k=-
（正值舍去）
直线l方程为y=-
x+1．
| yp |
| xp+1 |
| 1-xp |
| x-1 |
∵M是A1P1和A2P2的交点，所以
| yp |
| xp+1 |
| yp |
| 1-xp |
求得xm=
| 1 |
| xp |
| 1 |
| xm |
而yp=
| 1-xp2 |
| ||
| xm |
所以M点轨迹方程是x2-y2=1．
（2）设直线l方程为y=kx+1，
∴x2-（kx+1）2=1，
xc=
-k+
| ||
| k2-1 |
xb=
-k-
| ||
| k2-1 |
∵
| AC |
| AB |
将上面式子代入，解得k2=
| 9 |
| 5 |
因为直线l与曲线E交于y轴“右边”不同两点C，B，
所以k=-
| 3 | ||
|
直线l方程为y=-
| 3 | ||
|
点评：本题考查直线和圆锥曲线的综合应用，解题时要认真审题，仔细解答．
练习册系列答案
相关题目
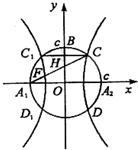如图，以A1，A2为焦点的双曲线E与半径为c的圆O相交于C，D，C1，D1，连接CC1与OB交于点H，且有：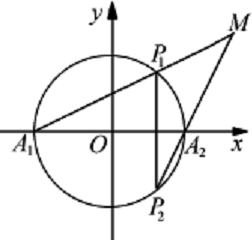
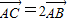，求直线l的方程．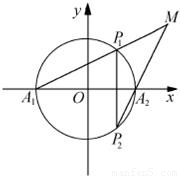
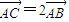，求直线l的方程．