题目内容
5.二次函数y=kx2(x>0)的图象在点(an,an2)处的切线与x轴交点的横坐标为an+1,n为正整数,a1=$\frac{1}{3}$,若数列{an}的前n项和为Sn,则S5=$\frac{31}{48}$.分析 由已知求出k=1,函数y=x2(x>0)的导数为y′=2x,由此利用导数的几何意义求出y=kx2在点(an,an2)处的切线方程,从而得到数列{an}是等比数列,公比q为$\frac{1}{2}$,由此能求出S5.
解答 解:∵二次函数y=kx2(x>0)的图象在点(an,an2)处的切线与x轴交点的横坐标为an+1,n为正整数,
∴${{a}_{n}}^{2}=k{{a}_{n}}^{2}$,解得k=1,
∴函数y=x2(x>0)的导数为y′=2x,
则在点(an,an2)处的切线方程为:y-an2=2an(x-an),
当y=0时,解得x=$\frac{1}{2}{a}_{n}$,
∴an+1=$\frac{1}{2}$an,即数列{an}是等比数列,公比q为$\frac{1}{2}$,
∵a1=$\frac{1}{3}$,∴S5=$\frac{\frac{1}{3}(1-\frac{1}{{2}^{5}})}{1-\frac{1}{2}}$=$\frac{31}{48}$.
故答案为:$\frac{31}{48}$.
点评 本题考查数列的前5项和的求法,是中档题,解题时要认真审题,注意导数的几何意义和等比数列性质的合理运用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.一个几何体的三视图如图所示,则该几何体的体积为( )
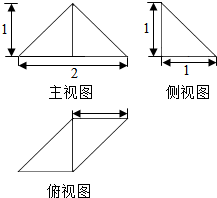

| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
20.阅读如图所示的程序框图,运行相应的程序,若输入x值为-4,则输出y值是( )

| A. | 7 | B. | 4 | C. | -1 | D. | 0 |
10.若集合A={y|y=2x},B={x|x2-2x-3>0,x∈R},那么A∩B=( )
| A. | (0,3] | B. | [-1,3] | C. | (3,+∞) | D. | (0,-1)∪(3,+∞) |