题目内容
如果关于x的不等式|x+1|+|x+2|≥k，对于?x∈R恒成立，则实数k的取值范围是（ ）
| A、[2，+∞] |
| B、（-1，+∞） |
| C、（-∞，1] |
| D、（3，8） |
考点：函数恒成立问题
专题：
分析：直接利用绝对值的几何意义求解|x+1|+|x+2|的最小值，则答案可求．
解答：
解：令f（x）=|x+1|+|x+2|，
而|x+1|+|x+2|的几何意义为数轴上动点X到两个定点-1，-2的距离的和，
如图：
由图可知，|x+1|+|x+2|的最小值为1．
∴实数k的取值范围是（-∞，1]．
故选：C．
而|x+1|+|x+2|的几何意义为数轴上动点X到两个定点-1，-2的距离的和，
如图：
由图可知，|x+1|+|x+2|的最小值为1．
∴实数k的取值范围是（-∞，1]．
故选：C．
点评：本题考查了函数恒成立问题，考查了绝对值的几何意义，是中档题．
练习册系列答案
计算高手系列答案
相关题目
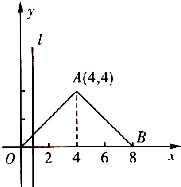如图所示，直线l⊥x轴，从原点开始向右平行移动到x=8处停止，它截△AOB所得左侧图形的面积为S，它与x轴的交点为（x，0）．