题目内容
设二次方程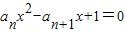 ,n∈N+有两根α和β,且满足6α-2αβ+6β=3,a1=1
,n∈N+有两根α和β,且满足6α-2αβ+6β=3,a1=1(1)试用an表示an+1;
(2)证明
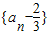 是等比数列;
是等比数列;(3)设
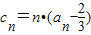 ,n∈N+,Tn为{cn}的前n项和,证明Tn<2,(n∈N*).
,n∈N+,Tn为{cn}的前n项和,证明Tn<2,(n∈N*).
【答案】分析:(1)由题设知6α-2αβ+6β=3,故即6• -2
-2 =3,由此能用an表示an+1.
=3,由此能用an表示an+1.
(2)由 ,n∈N+.知an+1-
,n∈N+.知an+1- =
= +
+ =
= ,由此能够证明
,由此能够证明 是等比数列.
是等比数列.
(3)由 是以
是以 为首项,以
为首项,以 为公比的等比数列,知
为公比的等比数列,知 =
= ,推出cn,由此利用错位相减法能够证明Tn<2.
,推出cn,由此利用错位相减法能够证明Tn<2.
解答:解:(1)∵二次方程 ,n∈N+有两根α和β,
,n∈N+有两根α和β,
且满足6α-2αβ+6β=3,a1=1,
∴6α-2αβ+6β=3,
即6• -2
-2 =3,
=3,
∴ ,n∈N+.
,n∈N+.
(2)∵ ,n∈N+.
,n∈N+.
∴an+1- =
= +
+ =
= ,
,
且 =
= ,
,
∴ 是以
是以 为首项,以
为首项,以 为公比的等比数列.
为公比的等比数列.
(3)∵ 是以
是以 为首项,以
为首项,以 为公比的等比数列,
为公比的等比数列,
∴ =
= ,cn=n•
,cn=n• ,
,
∴ +…+(n-1)•
+…+(n-1)• ],
],
 +…+(n-1)•
+…+(n-1)• +
+ n•
n• ,
,
两式相减,得
= -
- n•(
n•( )n
)n
Tn= -
-
 -
- n•
n• ,
,
整理,得Tn<2.
点评:本题考查数列的性质的综合运用,考查不等式的证明,综合性强,难度大,对数学思想的要求较高,解题时要认真审题,仔细解答,注意合理地进行等价转化.
 -2
-2 =3,由此能用an表示an+1.
=3,由此能用an表示an+1.(2)由
 ,n∈N+.知an+1-
,n∈N+.知an+1- =
= +
+ =
= ,由此能够证明
,由此能够证明 是等比数列.
是等比数列.(3)由
 是以
是以 为首项,以
为首项,以 为公比的等比数列,知
为公比的等比数列,知 =
= ,推出cn,由此利用错位相减法能够证明Tn<2.
,推出cn,由此利用错位相减法能够证明Tn<2.解答:解:(1)∵二次方程
 ,n∈N+有两根α和β,
,n∈N+有两根α和β,且满足6α-2αβ+6β=3,a1=1,
∴6α-2αβ+6β=3,
即6•
 -2
-2 =3,
=3,∴
 ,n∈N+.
,n∈N+.(2)∵
 ,n∈N+.
,n∈N+.∴an+1-
 =
= +
+ =
= ,
,且
 =
= ,
,∴
 是以
是以 为首项,以
为首项,以 为公比的等比数列.
为公比的等比数列.(3)∵
 是以
是以 为首项,以
为首项,以 为公比的等比数列,
为公比的等比数列,∴
 =
= ,cn=n•
,cn=n• ,
,∴
 +…+(n-1)•
+…+(n-1)• ],
], +…+(n-1)•
+…+(n-1)• +
+ n•
n• ,
,两式相减,得

=
 -
- n•(
n•( )n
)nTn=
 -
-
 -
- n•
n• ,
,整理,得Tn<2.
点评:本题考查数列的性质的综合运用,考查不等式的证明,综合性强,难度大,对数学思想的要求较高,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
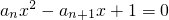 ,n∈N+有两根α和β,且满足6α-2αβ+6β=3,a1=1
,n∈N+有两根α和β,且满足6α-2αβ+6β=3,a1=1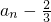 是等比数列;
是等比数列;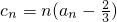 ,n∈N+,Tn为{cn}的前n项和,证明:
,n∈N+,Tn为{cn}的前n项和,证明: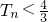 (n∈N+).
(n∈N+).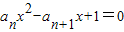 ,n∈N+有两根α和β,且满足6α-2αβ+6β=3,a1=1
,n∈N+有两根α和β,且满足6α-2αβ+6β=3,a1=1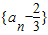 是等比数列;
是等比数列;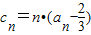 ,n∈N+,Tn为{cn}的前n项和,证明Tn<2,(n∈N*).
,n∈N+,Tn为{cn}的前n项和,证明Tn<2,(n∈N*).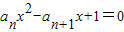 ,n∈N+有两根α和β,且满足6α-2αβ+6β=3,a1=1.
,n∈N+有两根α和β,且满足6α-2αβ+6β=3,a1=1.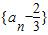 是等比数列,并求{an}的通项公式;
是等比数列,并求{an}的通项公式;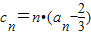 ,n∈N+,Tn为{cn}的前n项和,证明:Tn<2,(n∈N+).
,n∈N+,Tn为{cn}的前n项和,证明:Tn<2,(n∈N+).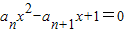 ,n∈N+有两根α和β,且满足6α-2αβ+6β=3,a1=1
,n∈N+有两根α和β,且满足6α-2αβ+6β=3,a1=1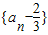 是等比数列;
是等比数列;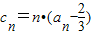 ,n∈N+,Tn为{cn}的前n项和,证明:
,n∈N+,Tn为{cn}的前n项和,证明: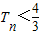 (n∈N+).
(n∈N+).