题目内容
(本题满分12分)
已知椭圆的中心在原点 ,焦点在坐标轴上,直线
,焦点在坐标轴上,直线 与该椭圆相交于
与该椭圆相交于 和
和 ,且
,且 ,
, ,求椭圆的方程.
,求椭圆的方程.
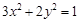 ,或
,或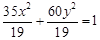 。
。
解析试题分析:设所求椭圆的方程为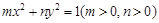 ,
,
根据OP⊥OQ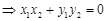
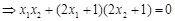
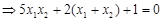 ,据此可得到一个m,n的方程,再根据弦长公式根据
,据此可得到一个m,n的方程,再根据弦长公式根据 ,得到m,n的另一个方程.然后解方程组可求出椭圆的方程.
,得到m,n的另一个方程.然后解方程组可求出椭圆的方程.
设所求椭圆的方程为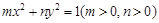 ,
,
依题意,点P(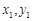 )、Q(
)、Q(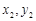 )的坐标满足方程组
)的坐标满足方程组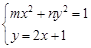
解之并整理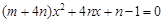 …………………………………2分;
…………………………………2分;
所以: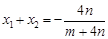 ,
,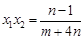 ①………………3分;
①………………3分;
由OP⊥OQ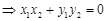
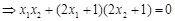
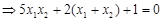
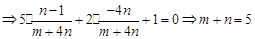 ②…………6分;
②…………6分;
又
|PQ|=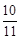
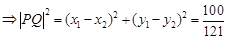
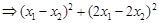 =
=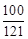
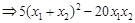 =
=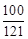
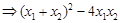 =
= ③………………9分;
③………………9分;
由①②③可得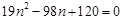
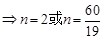
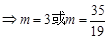 ………………11分;
………………11分;
故所求椭圆方程为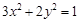 ,或
,或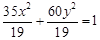 ………………12分..
………………12分..
考点:直线与椭圆的位置关系,弦长公式.
点评:本小题从方程的角度来考虑设出椭圆的方程,根据 ,
, 建立关于两个关于m,n的两个方程求出m,n从而得到椭圆的方程.
建立关于两个关于m,n的两个方程求出m,n从而得到椭圆的方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
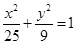 有相同的焦点,求此双曲线方程.
有相同的焦点,求此双曲线方程.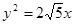 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点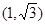 ,又知直线
,又知直线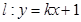 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.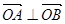 ,求实数k值.
,求实数k值. 与
与 轴相切,圆心
轴相切,圆心 上且在第二象限,直线
上且在第二象限,直线 过点
过点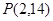 .
. 的方程;
的方程; 两点且
两点且 ,求直线
,求直线 的离心率为
的离心率为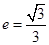 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线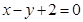 相切,
相切,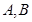 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点,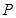 为椭圆
为椭圆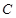 上的动点.
上的动点. 的斜率分别为
的斜率分别为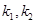 ,求
,求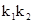 的值。
的值。 上的任意一点到它的两个焦点
上的任意一点到它的两个焦点 ,
, 
 的距离之和为
的距离之和为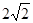 ,且其焦距为
,且其焦距为 .
. 的方程;
的方程; 与椭圆
与椭圆 .若存在,求出
.若存在,求出 的值;不存在,说明理由.
的值;不存在,说明理由. :
: (
( )的短轴长与焦距相等,且过定点
)的短轴长与焦距相等,且过定点 ,倾斜角为
,倾斜角为 的直线
的直线 交椭圆
交椭圆 、
、 两点.
两点. 轴上截距的范围.
轴上截距的范围. ,点
,点 在椭圆上。
在椭圆上。 ,直线
,直线 与椭圆交于A、B,且线段AB以M(1,1)为中点,求直线
与椭圆交于A、B,且线段AB以M(1,1)为中点,求直线 (a>b>0)的离心率
(a>b>0)的离心率 ,过点
,过点 和
和 的直线与原点的距离为
的直线与原点的距离为 .
.
 ,若直线
,若直线 与椭圆交于
与椭圆交于 、
、 两 点.问:是否存在
两 点.问:是否存在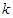 的值,
的值, 为直径的圆过
为直径的圆过 点?请说明理由.
点?请说明理由.