题目内容
(本小题14分)已知椭圆 的离心率为
的离心率为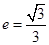 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线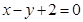 相切,
相切,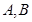 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点,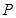 为椭圆
为椭圆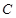 上的动点.
上的动点.
(1)求椭圆的标准方程;
(2)若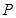 与
与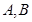 均不重合,设直线
均不重合,设直线 的斜率分别为
的斜率分别为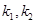 ,求
,求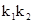 的值。
的值。
(1) (2)
(2)
解析试题分析:(1)由题意可得圆的方程为 直线
直线 与圆相切,
与圆相切, 即
即 又
又
即 得
得
所以椭圆方程为
(2)设
 则
则
即
则

即
 的值为
的值为
考点:椭圆的标准方程的求法;椭圆的简单性质;圆的简单性质;点到直线的距离公式;斜率公式;
点评:熟记椭圆中 的关系式,并灵活应用。注意椭圆中
的关系式,并灵活应用。注意椭圆中 的关系式与双曲线中
的关系式与双曲线中 的关系式的不同。此题属于基础题型。
的关系式的不同。此题属于基础题型。

练习册系列答案
相关题目
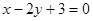 和
和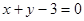 的交点,且满足下列条件的直线
的交点,且满足下列条件的直线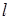 的方程.
的方程.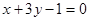 垂直;
垂直;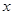 轴,
轴,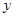 轴上的截距相等.
轴上的截距相等.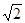 ,离心率为0.6,求椭圆的标准方程。
,离心率为0.6,求椭圆的标准方程。 中心在原点,一个焦点为
中心在原点,一个焦点为 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是 。
。 的直线
的直线 ,使直线
,使直线 与直线
与直线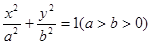 ,离心率为
,离心率为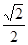 的椭圆经过点
的椭圆经过点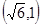 .
. 分别与椭圆交于
分别与椭圆交于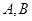 和
和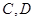 ,是否存在常数
,是否存在常数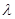 ,使得
,使得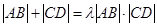 ?若存在,求出实数
?若存在,求出实数 ,焦点在坐标轴上,直线
,焦点在坐标轴上,直线 与该椭圆相交于
与该椭圆相交于 和
和 ,且
,且 ,
, ,求椭圆的方程.
,求椭圆的方程.  ,焦点为
,焦点为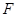 ,顶点为
,顶点为 ,点
,点 在抛物线上移动,
在抛物线上移动,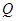 是
是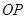 的中点,
的中点,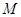 是
是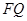 的中点,求点
的中点,求点
 中,点
中,点 到两点
到两点 ,
, 的距离之和等于
的距离之和等于 ,设点
,设点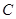 。
。 作两条互相垂直的直线
作两条互相垂直的直线 分别与曲线
分别与曲线 和
和 。
。 为直径的圆过能否过坐标原点,若能求出此时的
为直径的圆过能否过坐标原点,若能求出此时的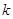 值,若不能说明理由;
值,若不能说明理由; 面积的取值范围。
面积的取值范围。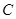 的顶点为坐标原点,焦点在
的顶点为坐标原点,焦点在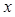 轴上. 且经过点
轴上. 且经过点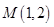 ,
,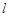 过点
过点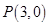 ,交抛物线
,交抛物线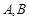 两点,是否存在垂直于
两点,是否存在垂直于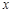 轴的直线
轴的直线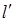 被以
被以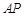 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出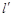 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.