题目内容
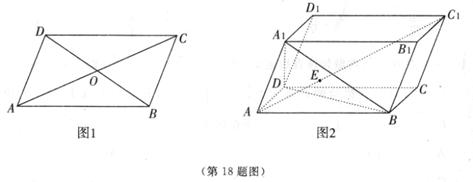
如图所示,平行六面体ABCD—A1B1C1D1中,以顶点A为端点的三条棱长度都为1,且两
两夹角为60°.
(1)求AC1的长;
(2)求BD1与AC夹角的余弦值.

(1) AC1的长为![]() (2) AC与BD1夹角的余弦值为
(2) AC与BD1夹角的余弦值为![]()
解析:
记![]() =a,
=a,![]() =b,
=b,![]() =c,
=c,
则|a|=|b|=|c|=1,〈a,b〉=〈b,c〉=〈c,a〉=60°,
∴a·b=b·c=c·a=![]() .
.
(1)|![]() |2=(a+b+c)2
|2=(a+b+c)2
=a2+b2+c2+2(a·b+b·c+c·a)
=1+1+1+2×(![]() +
+![]() +
+![]() )=6,
)=6,
∴|![]() |=
|=![]() ,即AC1的长为
,即AC1的长为![]() .
.
(2)![]() =b+c-a,
=b+c-a,![]() =a+b,
=a+b,
∴|![]() |=
|=![]() ,|
,|![]() |=
|=![]() ,
,
![]() ·
·![]() =(b+c-a)·(a+b)
=(b+c-a)·(a+b)
=b2-a2+a·c+b·c=1.
∴cos〈![]() ,
,![]() 〉=
〉= =
=![]() .
.
∴AC与BD1夹角的余弦值为![]() .
.

练习册系列答案
相关题目

 ,那么在图②中所示的平行六面体
,那么在图②中所示的平行六面体 中,
中, 等于( )
等于( )





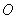 是平行四边形
是平行四边形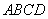 对角线的交点,若
对角线的交点,若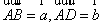 ,则
,则 ,(2)在图2所示的平行六面体(底面是平行四边形的棱柱)
,(2)在图2所示的平行六面体(底面是平行四边形的棱柱)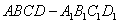 中,
中,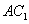 与截面
与截面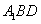 的交点为
的交点为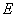 ,设
,设 。类比(1)写出用
。类比(1)写出用 表示
表示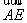 的关系式是 。
的关系式是 。