题目内容
16. 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.(1)证明:PA∥平面EDB;
(2)求VB-EFD.
分析 (1)利用线面平行的判定定理证明线面平行.
(2)利用锥体的体积公式求体积.
解答  解:(1)连结AC,交BD于O,连结EO,
解:(1)连结AC,交BD于O,连结EO,
因为ABCD是正方形,点O是AC的中点,在三角形PAF中,EO是中位线,
所以PA∥EO,而EO?面EDB,且PA?面EDB,所以PA∥平面EDB;
(2)因为PD=DC=2,所以PC=2$\sqrt{2}$,PB=2$\sqrt{3}$,PE=$\sqrt{2}$,
因为$\frac{EF}{PE}=\frac{BC}{PB}$,所以EF=$\frac{\sqrt{6}}{3}$,PF=$\frac{2\sqrt{3}}{3}$,FB=2$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
DF=$\sqrt{B{D}^{2}-P{F}^{2}}$=$\frac{2\sqrt{6}}{3}$,DE=$\sqrt{2}$,BF=$\sqrt{B{D}^{2}-D{F}^{2}}$=$\frac{4\sqrt{3}}{3}$,
所以VB-EFD=$\frac{1}{3}$×$\frac{1}{2}$×DE×EF×BF=$\frac{4}{9}$.
点评 本题主要考查线面平行的判定,考查锥体的体积公式,要求熟练掌握相应的判定定理.

练习册系列答案
相关题目
7.点A(sin2016°,cos2016°)在直角坐标平面上位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.向量$\overrightarrow{a}$=(1,2,3),则|$\overrightarrow{a}$|=( )
| A. | $\sqrt{15}$ | B. | $\sqrt{14}$ | C. | $\sqrt{13}$ | D. | $\sqrt{12}$ |
11.用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+7x2+8x+1,当x=4时,需要做乘法和加法的次数分别是( )
| A. | 6,6 | B. | 5,6 | C. | 5,5 | D. | 6,5 |
8.若三点A(2,2),B(a,0),C(0,4)共线,则a的值等于( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
5.口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.38,摸出白球的概率是0.34,那么摸出黑球的概率是( )
| A. | 0.42 | B. | 0.28 | C. | 0.36 | D. | 0.62 |
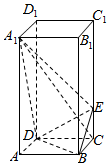 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.