题目内容
(本小题满分12分)
已知椭圆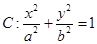
 的离心率为
的离心率为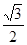 ,直线
,直线 经过椭圆的上顶点
经过椭圆的上顶点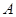 和右顶点
和右顶点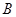 ,并且和圆
,并且和圆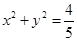 相切.
相切.
(1)求椭圆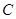 的方程;
的方程;
(2)设直线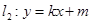
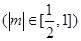 与椭圆
与椭圆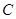 相交于
相交于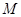 ,
,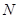 两点,以线段
两点,以线段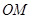 ,
, 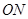 为邻边作平行四边行
为邻边作平行四边行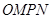 ,其中顶点
,其中顶点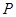 在椭圆
在椭圆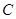 上,
上,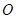 为坐标原点,求
为坐标原点,求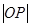 的取值范围.
的取值范围.
已知椭圆
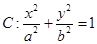
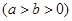 的离心率为
的离心率为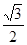 ,直线
,直线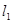 经过椭圆的上顶点
经过椭圆的上顶点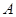 和右顶点
和右顶点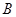 ,并且和圆
,并且和圆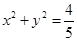 相切.
相切.(1)求椭圆
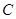 的方程;
的方程;(2)设直线
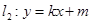
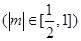 与椭圆
与椭圆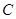 相交于
相交于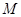 ,
,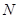 两点,以线段
两点,以线段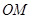 ,
, 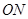 为邻边作平行四边行
为邻边作平行四边行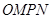 ,其中顶点
,其中顶点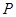 在椭圆
在椭圆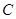 上,
上,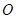 为坐标原点,求
为坐标原点,求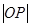 的取值范围.
的取值范围.(1)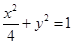
(2)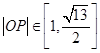
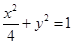
(2)
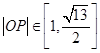
本试题主要是考查了椭圆方程的求解,以及直线与椭圆的位置关系的综合运用。
(1)因为椭圆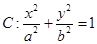
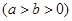 的离心率为
的离心率为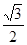 ,直线
,直线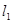 经过椭圆的上顶点
经过椭圆的上顶点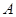 和右顶点
和右顶点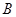 ,并且和圆
,并且和圆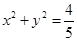 相切.
相切.
结合椭圆的性质和线与圆的位置关系得到参数a,b,c的表达式,得到椭圆的方程。
(2)根据直线方程与椭圆方程联立方程组,结合韦达定理表示出点P的坐标,然后点P在椭圆上得到参数的关系式,,利用m的范围得到op 的范围。
解:(1)由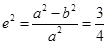 得
得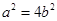 ,所以
,所以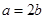 ……………………1分
……………………1分
所以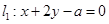 ,有
,有 ,解得
,解得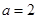 ………..5分
………..5分
所以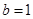 ,所以椭圆方程为
,所以椭圆方程为 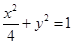 …………………………….6分
…………………………….6分
(2)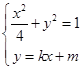 , 消去
, 消去 得:
得: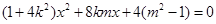
设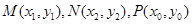
则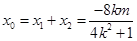 ,
,  ,
,
故点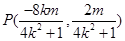 …………………………………………………9分
…………………………………………………9分
点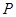 在椭圆上,有
在椭圆上,有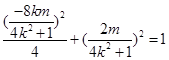 ,整理得
,整理得
所以 ,
,
而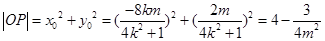 ,………….11分
,………….11分
因为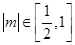 ,所以
,所以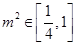 ,所以
,所以 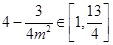 ,
,
所以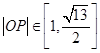 …………………………………………………………….12分
…………………………………………………………….12分
(1)因为椭圆
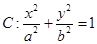
 的离心率为
的离心率为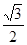 ,直线
,直线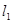 经过椭圆的上顶点
经过椭圆的上顶点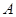 和右顶点
和右顶点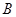 ,并且和圆
,并且和圆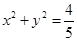 相切.
相切.结合椭圆的性质和线与圆的位置关系得到参数a,b,c的表达式,得到椭圆的方程。
(2)根据直线方程与椭圆方程联立方程组,结合韦达定理表示出点P的坐标,然后点P在椭圆上得到参数的关系式,,利用m的范围得到op 的范围。
解:(1)由
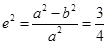 得
得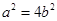 ,所以
,所以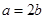 ……………………1分
……………………1分所以
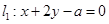 ,有
,有 ,解得
,解得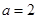 ………..5分
………..5分所以
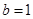 ,所以椭圆方程为
,所以椭圆方程为 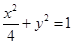 …………………………….6分
…………………………….6分(2)
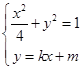 , 消去
, 消去 得:
得: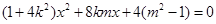
设
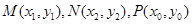
则
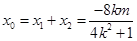 ,
,  ,
,故点
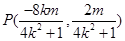 …………………………………………………9分
…………………………………………………9分点
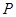 在椭圆上,有
在椭圆上,有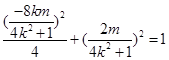 ,整理得
,整理得
所以
 ,
,而
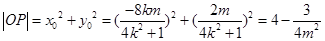 ,………….11分
,………….11分因为
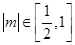 ,所以
,所以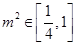 ,所以
,所以 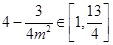 ,
,所以
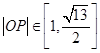 …………………………………………………………….12分
…………………………………………………………….12分
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
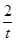 )(t∈R , t≠ 0)为圆心的圆与
)(t∈R , t≠ 0)为圆心的圆与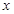 轴交于点O, A,
轴交于点O, A,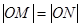 ,求圆C的方程.
,求圆C的方程.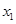 、
、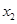 是关于x的方程
是关于x的方程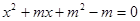 的两个不相等的实数根,那么过两点
的两个不相等的实数根,那么过两点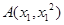 ,
,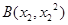 的直线与圆
的直线与圆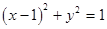 的位置关系是( )
的位置关系是( )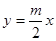 与圆
与圆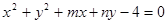 交于
交于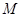 、
、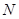 两点,且
两点,且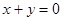 对称,则弦
对称,则弦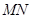 的长为( )
的长为( ) 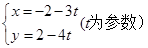 它与曲线C:
它与曲线C: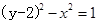 交于A、B两点。
交于A、B两点。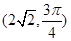 ,求点P到线段AB中点M的距离。
,求点P到线段AB中点M的距离。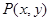 是圆
是圆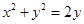 上的动点,
上的动点,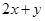 的取值范围;
的取值范围;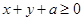 恒成立,求实数
恒成立,求实数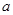 的取值范围。
的取值范围。 :
: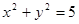 和点
和点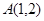 ,则过
,则过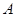 且与圆
且与圆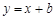 交圆
交圆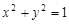 于A、B两点,且
于A、B两点,且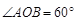 (O为原点),则实数
(O为原点),则实数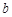 的值为 .
的值为 . :y="k" (x+2
:y="k" (x+2 )与圆O:
)与圆O: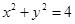 相交于A、B两点,O是坐标原点,
相交于A、B两点,O是坐标原点, ABO的面积为S.
ABO的面积为S.