题目内容
【题目】已知函数
的图像过点
，且对任意的
都有不等式
成立.若函数
有三个不同的零点，则实数
的取值范围是__________________.
【答案】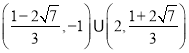
【解析】
首先由函数的性质确定函数
的解析式，然后将原问题转化为两个函数有三个交点的问题，考查临界条件，求得临界值即可确定实数
的取值范围.
注意到
时,
,
即
是函数
的切线，且切点坐标为
，
据此结合题意可知：是函数
的切线，且切点坐标为，
由函数的解析式有
，故：
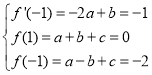，解得：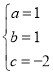
，
则函数的解析式为
，
函数
有三个不同的零点，
则函数
与函数
有三个不同的交点，
注意到
，
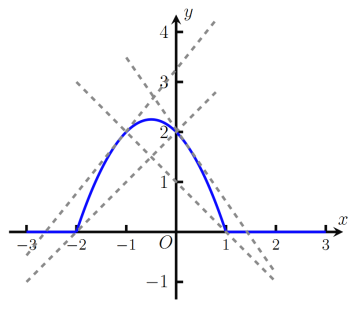
绘制函数图像如图所示，考查如图所示的临界情况，
当函数
与函数
只有两个交点时：
若一次函数过点
，则：
且
,解得
；
若一次函数过点
，则：
且
,解得
；
若一次函数与二次函数在区间
内相切，
由
可得
，
设切点坐标为
，则切线的斜率为：
，
切线方程为：
，
整理可得：
，
由于，考查一次函数斜率与
轴截距的关系可得：
，解得：
，
则切线的斜率为：
.
综上可得：实数的取值范围是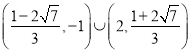
.
练习册系列答案
相关题目
