题目内容
设非空集合S具有如下性质:
①元素都是正整数;②若x∈S,则10-x∈S.
(1)请你写出符合条件,且分别含有1个、2个、3个元素的集合S各一个.
(2)是否存在恰有6个元素的集合S?若存在,写出所有的集合S;若不存在,请说明理由.
(3)由(1)、(2)的解答过程启发我们,可以得出哪些关于集合S的一般性结论(要求至少写出两个结论)?
[解析] (1)由题意可知,若集合S中含有一个元素,则应满足10-x=x,即x=5,故S={5}.
若集合S中含有两个元素,设S={a,b},则a,b∈N+,且a+b=10,故S可以是下列集合中的一个:
{1,9},{2,8},{3,7},{4,6},
若集合S中含有3个元素,由集合S满足的性质可知5∈S,故S是{1,5,9}或{2,5,8}或{3,5,7}或{4,5,6}中的一个.
(2)存在含有6个元素的非空集合S如下所示:
S={1,2,3,7,8,9}或S={1,2,4,6,8,9}或S={1,3,4,6,7,9}或S={2,3,4,6,7,8}共4个.
(3)答案不唯一,如:①S⊆{1,2,3,4,5,6,7,8,9};②若5∈S,则S中元素个数为奇数个,若5∉S,则S中元素个数为偶数个.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
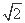 ,则圆C的标准方程为 .
,则圆C的标准方程为 . 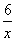 ∈N}是有限集.其中正确命题的个数是( )
∈N}是有限集.其中正确命题的个数是( )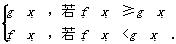 则F(x)的最值是( )
则F(x)的最值是( )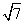 ,无最小值
,无最小值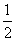 absinC计算a=2、b=1、C=60°时三角形的面积;
absinC计算a=2、b=1、C=60°时三角形的面积;