题目内容
15.已知函数f(x)=ax2+x-a(a∈R)(1)若函数f(x)有最大值$\frac{17}{8}$,求实数a的值;
(2)解不等式f(x)>1(用a表示)
(3)若x>1时,恒有f(x)>0成立,求a的取值范围.
分析 (1)由题意知$\left\{\begin{array}{l}{a<0}\\{a•(-\frac{1}{2a})^{2}-\frac{1}{2a}-a=\frac{17}{8}}\end{array}\right.$,从而解得;
(2)分类讨论,从而解不等式f(x)>1;
(3)分类讨论,从而分别判断一次函数与二次函数的性质并判断,从而求得.
解答 解:(1)∵函数f(x)有最大值$\frac{17}{8}$,
∴$\left\{\begin{array}{l}{a<0}\\{a•(-\frac{1}{2a})^{2}-\frac{1}{2a}-a=\frac{17}{8}}\end{array}\right.$,
解得,a=-2或a=-$\frac{1}{8}$;
(2)当a=0时,f(x)=x>1;
当a>0时,ax2+x-a>1,
即(x-1)(ax+a+1)>0;
故x>1或x<-$\frac{a+1}{a}$=-1-$\frac{1}{a}$;
当a<0时,ax2+x-a>1,
即a(x-1)(x+$\frac{a+1}{a}$)>0,
即(x-1)(x+$\frac{a+1}{a}$)<0;
当-1=$\frac{a+1}{a}$,即a=-$\frac{1}{2}$时,不等式无解;
当-$\frac{1}{2}$<a<0时,$\frac{a+1}{a}$<-1,
故1<x<-$\frac{a+1}{a}$;
当a<-$\frac{1}{2}$时,$\frac{a+1}{a}$>-1,
故-$\frac{a+1}{a}$<a<1;
(3)当a=0时,f(x)>0在x>1时恒成立;
当a≠0时,$\left\{\begin{array}{l}{a>0}\\{a+1-a≥0}\end{array}\right.$,
解得,a>0;
故a≥0.
点评 本题考查了函数的性质与不等式的关系应用及恒成立问题与最值问题的应用.

| A. | (1,2) | B. | (-2,2) | C. | (-1,5) | D. | (-2,5) |
| A. | 2 | B. | $\frac{1}{2}$ | C. | 3 | D. | $\frac{1}{3}$ |
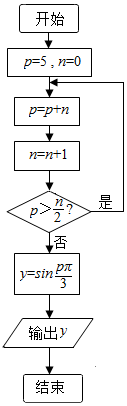
| A. | 1 | B. | 0 | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
| 分数 | [50,59) | [60,69) | [70,79) | [80,89) | [90,100] |
| 甲班频数 | 5 | 6 | 4 | 4 | 1 |
| 乙班频数 | 1 | 3 | 6 | 5 | 5 |
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
临界值表:
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |