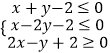题目内容
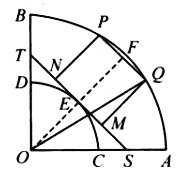
【题目】如图,已知![]() ,
, ![]() 分别是
分别是![]() 中点,弧
中点,弧![]() 的半径分别为
的半径分别为![]() ,点
,点![]() 平分弧
平分弧![]() ,过点
,过点![]() 作弧
作弧![]() 的切线分别交
的切线分别交![]() 于点
于点![]() .四边形
.四边形![]() 为矩形,其中点
为矩形,其中点![]() 在线段
在线段![]() 上,点
上,点![]() 在弧
在弧![]() 上,延长
上,延长![]() 与
与![]() 交于点
交于点![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
(1)求![]() 的解析式并求其定义域;
的解析式并求其定义域;
(2)求![]() 的最大值.
的最大值.
【答案】(1)![]() ,
, ![]() (2)
(2)![]()
【解析】试题分析:(1)由圆的性质得![]() 是
是![]() 中点,在
中点,在![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴![]() ,根据
,根据![]() 可得
可得![]() ,∴
,∴![]() ,又
,又![]() 为锐角,可得定义域为
为锐角,可得定义域为![]() ;(2)换元化简可得
;(2)换元化简可得![]() ,根据二次函数的单调性可求得
,根据二次函数的单调性可求得![]() .
.
试题解析:(1)∵![]() ,又
,又![]() ,
,
∴![]() ,由圆的性质得
,由圆的性质得![]() 是
是![]() 中点.
中点.
依题意得弧![]() 的半径分别为2,1
的半径分别为2,1
在![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,
,
∴![]() .
.
∵![]() ,
, ![]() 平分
平分![]() ,所以
,所以![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,∴
,∴ ![]() 即
即![]()
∴![]() ,又
,又![]() 为锐角,∴
为锐角,∴![]() .
.
所以![]() 的定义域为
的定义域为![]() .
.
(2)因为![]()
令![]() ,
,
∵![]() ,∴
,∴ ,则
,则![]() 在
在 上单调递增,
上单调递增,
∴ ,
,
∴![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目